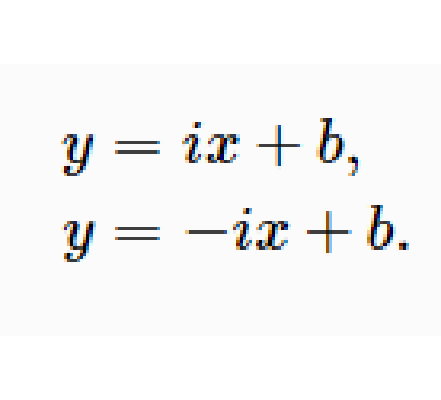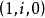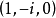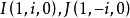基本介紹
- 中文名:迷向直線
- 外文名:isotropic line
- 別稱:極小直線
- 所屬學科:數學
- 所屬問題:高等幾何(射影幾何)
基本介紹,定義,分類,相關定理,
基本介紹
定義
定理1 平面內任何一圓通過無窮遠直線上兩個固定的共軛虛點。
顯然,兩圓點的線坐標方程為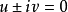 或
或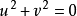 。
。
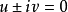
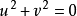
定義2 過平面內任意一點至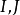 兩點的兩條直線,稱為該點的迷向直線(極小直線)。
兩點的兩條直線,稱為該點的迷向直線(極小直線)。
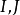
由定義可知,平面內任一點都有兩條迷向直線,因而,平面內所有的點的迷向直線構成以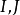 為中心的兩個平行線束。因此,平面內只有兩個迷向方向。當然它們都是虛直線,實際上是畫不出來的。
為中心的兩個平行線束。因此,平面內只有兩個迷向方向。當然它們都是虛直線,實際上是畫不出來的。
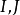
分類
以k為斜率的直線上的無窮遠點的坐標是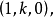 由此可知,兩條迷向直線的斜率分別為
由此可知,兩條迷向直線的斜率分別為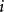 和
和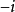 ,所以迷向直線的方程分別為
,所以迷向直線的方程分別為
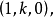
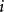
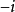
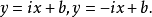
從而迷向方向分為兩類,一類是斜率是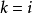 的,另一類是
的,另一類是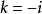 的。
的。
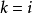
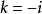
相關定理
定理3每一條迷向直線與任意一條直線的交角是不確定的。
證明:(1)設有兩條同類迷向直線,它們的斜率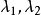 同為
同為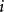 (或
(或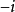 ),則
),則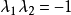 。由兩條直線的交角公式
。由兩條直線的交角公式
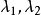
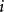
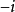
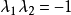
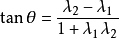
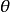
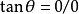
(2) 設有一條迷向直線,斜率為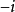 ,另一條是不同類的迷向直線或不是迷向直線,斜率為
,另一條是不同類的迷向直線或不是迷向直線,斜率為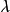 (
(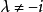 ),則由交角公式得
),則由交角公式得
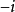
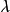
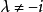
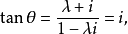
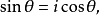
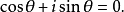
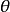
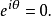
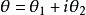
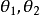
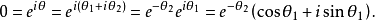
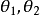
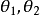
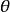
從定理3知,迷向直線的方向不能用角度表示,只能用斜率來表示。
定理4 (拉格爾Laguerre,1834-1886)設兩條非迷向直線的交角為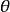 ,這兩條直線與過其交點的兩條以
,這兩條直線與過其交點的兩條以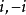 為斜率的迷向直線所成的交比為
為斜率的迷向直線所成的交比為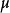 ,則在對數函式的主值範圍內必有
,則在對數函式的主值範圍內必有
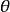
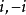
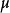
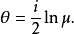
定理5兩條非迷向直線垂直的充要條件是這兩條直線被過交點的兩條迷向直線調和共軛。