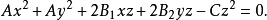虛圓點

虛圓點（circular points at infinity）也稱為圓點，是射影幾何中的名詞，是指在復射影平面上二個特殊的無窮遠點，也是每一個實數的圓在復化後都會包括的點，其齊次坐標為 (1, i, 0) 及 (1, −i, 0)。

基本介紹

• 中文名：虛圓點
• 外文名：circular points at infinity
• 領域：幾何

齊次坐標

復射影平面下的點可以用齊次坐標來表示，由複數組成的三元組(x:y:z)（其中x、y、z不全為0），若一個三元組乘以一個非零係數後和另一個三元組相等，二個三元組表示平面中的同一個點。在齊次坐標下，無窮遠處的點可以用z座標為0來表示。虛圓點的二個座標一般會表示為以下的齊次坐標：(1: i: 0)及(1: −i: 0)。

復化的圓

實數的圓，其中心點為x₀,y₀，直徑r（這三個數都是實數）可以描述為以下方程式解的集合：

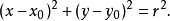
若轉換為齊次方程，且考慮所有複數的解，即得到復化的圓。虛圓點是所有復化的圓的交點。這二個點滿足以下的齊次方程式：

方程式中若所有的係數都是實數，此即為一般圓（在實射影平面）下的方程。若任一代數曲線通過上述兩點，即稱為圓代數曲線。