基本介紹
簡單n線形指n條直線(其中無三線共點)及其兩兩順次相交的交點所構成的圖形,這n條直線稱為邊,n個交點稱為頂點。簡單n點形是指n個點(其中無三點共線)及其兩兩順次連線所構成的圖形,這n個點稱為頂點,n條直線稱為邊。
如果一個簡單n點形的n個頂點都在一條
二次曲線上,則稱這個簡單n點形內接於一條二次曲線。
我們將簡單六點形
簡記為123456,而12,45;23,56;34,61稱為其三對對邊。
對於簡單n點(線)形,表1和表2分別給出了n=3和n=4的情形,顯然,對於給定的n個點(或n條直線),由它們所構成的簡單n點形(簡單n線形)與這n個點(n條直線)的排序有關。此外,這兩類圖形與初等幾何中的多邊形也是不同的概念。
相關定理
巴士卡(Pascal)定理
對於任意一個內接於非退化的二階曲線的簡單六點形,它的三對對邊的交點在一條直線上(如圖1)。這條直線稱為該二階曲線的巴士卡線。
 圖1
圖1巴士卡定理的逆定理
若簡單六點形的三對對邊的交點在一條直線上,則該簡單六點形內接於一條二階曲線。巴士卡定理是巴士卡(1623-1662)於1639年發現的,1806年布利安香(1785-1864)發現了其對偶定理。
布利安香(Brianchon)定理 對於任意一個外切於非退化的二級曲線的簡單六線形,它的三對對頂點的連線過一個點(如圖2)。這個點稱為該二級曲線的布利安香點。
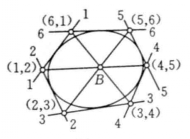 圖2
圖2布利安香(Brianchon)定理的逆定理也成立。
巴士卡定理的極限形式
所謂極限形式,是指簡單六點形有某些相鄰頂點重合,內接簡單六點形實際上成為簡單五點形,四點形,三點形。此時,連結重合的相鄰頂點的邊成為切線,將切線作為邊,套用巴士卡定理即可。
1.一對相鄰頂點重合,五點形情形
定理1 內接於非退化二階曲線的簡單五點形某點處的切線與其對邊的交點必在其餘兩對不相鄰邊的交點連線上(如圖3)。
 圖3
圖32.兩對相鄰頂點重合,四點形情形
將四點形的一對對頂點視為重合頂點時,有
定理2內接於一條非退化的二階曲線的簡單四點形兩對對邊的交點及其對頂點的切線的交點必共線(如圖4)。
將四點形的一對相鄰頂點視為重合頂點時,有
定理3內接於一條非退化二階曲線的簡單四點形,一對對邊的交點與其對頂點的切線的交點,三點共線(如圖4)。
 圖4
圖43.三對相鄰頂點重合,三點形情形
定理4 內接於一條非退化的二階曲線的三點形,其每一頂點的切線與對邊的交點,三點共線(如圖5)。
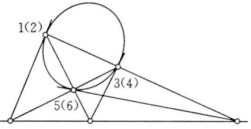 圖5
圖5當二階曲線退化時,巴士卡定理在一定情形下也成立。
例如,二階曲線退化成兩條直線,若六個點分為兩組,設三點1、3、5在一條直線上,而另有三點2、4、6在另一條直線上,則三個交點L=12×45、M=23×56、N=34×61也在一條直線上(如圖6)。本結論正是巴卜斯定理。
 圖6
圖6
 圖1
圖1 圖2
圖2 圖3
圖3 圖4
圖4 圖5
圖5 圖6
圖6
