簡單四點形(simple quadrangle)是一種簡單的n點形,指由平面上四個點A,B,C,D(其中無三點共線)及它們順次兩兩連結的直線AB,BC,CD,DA所組成的圖形稱為簡單四點形,記為簡單四點形ABCD,A,B,C,D稱為它的頂點,直線AB,BC,CD,DA稱為它的邊,不相鄰的頂點的連線AC,BD稱為它的對頂線。
基本介紹
基本介紹
 圖2
圖2相關定理
 圖2帕斯卡線
圖2帕斯卡線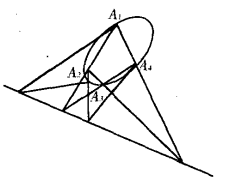 圖3
圖3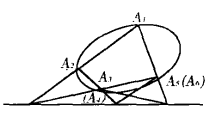 圖4
圖4完全四點形與簡單四點形的關係
 圖5
圖5
簡單四點形(simple quadrangle)是一種簡單的n點形,指由平面上四個點A,B,C,D(其中無三點共線)及它們順次兩兩連結的直線AB,BC,CD,DA所組成的圖形稱為簡單四點形,記為簡單四點形ABCD,A,B,C,D稱為它的頂點,直線AB,BC,CD,DA稱為它的邊,不相鄰的頂點的連線AC,BD稱為它的對頂線。
 圖2
圖2 圖2帕斯卡線
圖2帕斯卡線 圖3
圖3 圖4
圖4 圖5
圖5簡單四點形(simple quadrangle)是一種簡單的n點形,指由平面上四個點A,B,C,D(其中無三點共線)及它們順次兩兩連結的直線AB,BC,CD,DA所組成的圖形稱為簡單...
簡單n點形(simple n-gon)是一種簡單的平面圖形,即由平面上的n個點(n≥3,其中無三點共線)及它們順次兩兩連結的n條直線所組成的平面圖形,這n個點稱為簡單n...
完全n點形(complete n-gon)是一種簡單的平面圖形,即由平面上的n個點(n≥3,其中無三點共線)及它們每兩個點的連線所組成的平面圖形,這n個點稱為完全n點形...
完全四點形(complete quadrangle)是一種特殊的完全n點形。由平面上四個點(其中無三點共線)及其兩兩連結的六條直線所組成的圖形稱為完全四點形。這四個點稱為...
如果同一平面內的四個點在同一個圓上,則稱這四個點共圓,一般簡稱為“四點共圓”。四點共圓有三個性質:(1)共圓的四個點所連成同側共底的兩個三角形的...
簡單n線形(simple n-side)是一種簡單的平面圖形,即由平面上的n條直線(n≥3,其中無三線共點)及它們順次兩兩的交點所組成的平面圖形,這n條直線稱為簡單n線形...
對偶圖形簡單四線形 由四條直線(其中無三線共點)以及其中任意兩條直線的六個交點所組成的圖形叫完全四邊形(右圖b)。這四條直線叫邊,六個點叫頂點,不在公共邊...
完全n線形(complete n-side)是一種簡單的平面圖形,是由平面上的n條直線(n≥3,其中無三線共點)及它們每兩條直線的交點所組成的平面圖形。這n條直線稱為完全n...
