基本介紹
- 中文名:完全四點形
- 外文名:complete quadrangle
- 領域:數學
- 屬性:一種特殊的完全n點形
- 套用:高等幾何
- 性質:三點共線理論、調和性等
完全四點形定義及其性質
完全四點形中三點共線理論
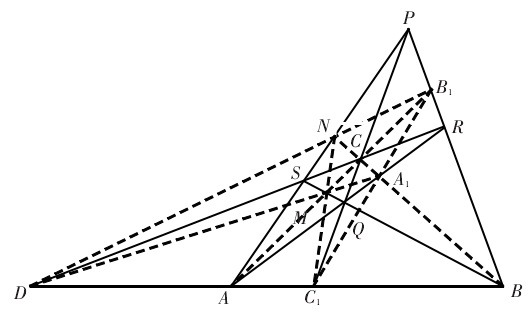 圖1 完全四點形的三點共線圖
圖1 完全四點形的三點共線圖完全四點形的調和性
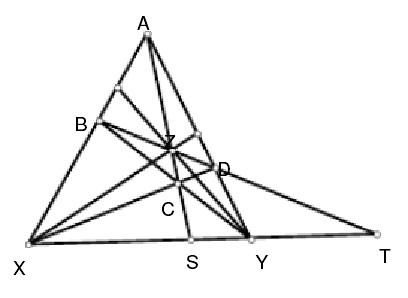 圖2
圖2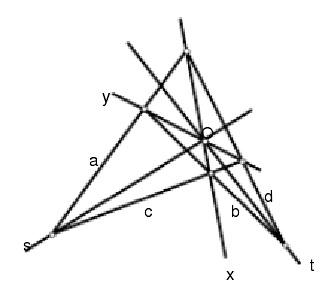 圖3
圖3調和性在初等幾何中的套用
解決平分角問題
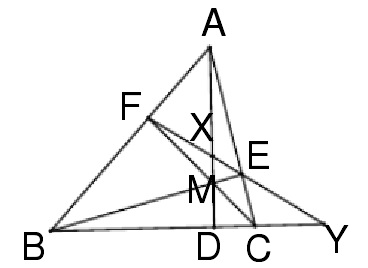 圖4
圖4解決平分線段問題
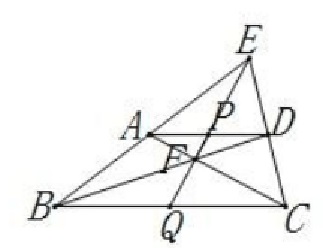 圖5
圖5解決點共線問題
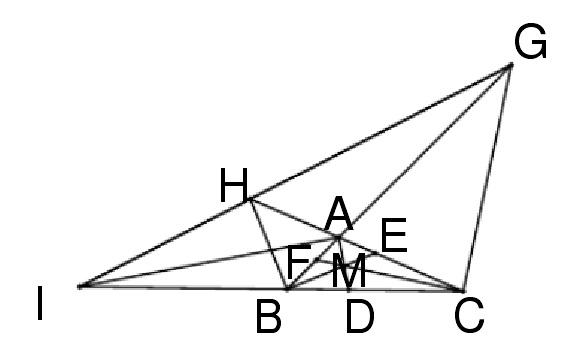 圖6
圖6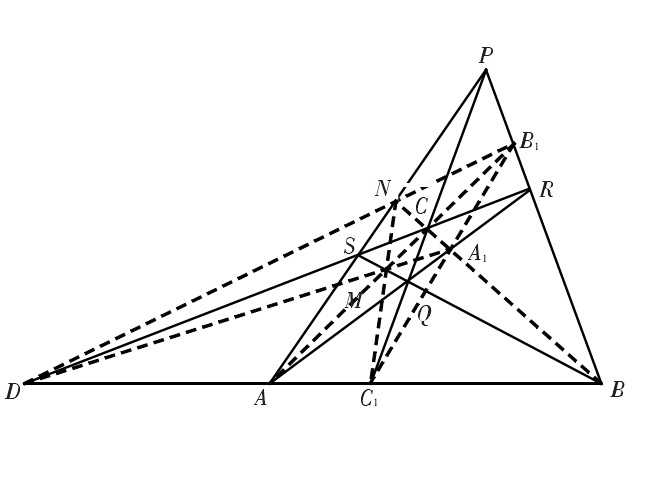
 圖1 完全四點形的三點共線圖
圖1 完全四點形的三點共線圖 圖2
圖2 圖3
圖3 圖4
圖4 圖5
圖5 圖6
圖6完全四點形(complete quadrangle)是一種特殊的完全n點形。由平面上四個點(其中無三點共線)及其兩兩連結的六條直線所組成的圖形稱為完全四點形。這四個點稱為...
完全n點形(complete n-gon)是一種簡單的平面圖形,即由平面上的n個點(n≥3,其中無三點共線)及它們每兩個點的連線所組成的平面圖形,這n個點稱為完全n點形...
簡單四點形(simple quadrangle)是一種簡單的n點形,指由平面上四個點A,B,C,D(其中無三點共線)及它們順次兩兩連結的直線AB,BC,CD,DA所組成的圖形稱為簡單...
完全n線形(complete n-side)是一種簡單的平面圖形,是由平面上的n條直線(n≥3,其中無三線共點)及它們每兩條直線的交點所組成的平面圖形。這n條直線稱為完全n...
在數學,尤其是射影幾何學裡,完全四線形是指歐幾里德平面上由四條兩兩相交但是任意三條不共點的直線加上它們的六個交點組成的圖形。相應地,由四個三三不共線...
四點青鱗編輯 鎖定 本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!體呈長卵圓形,側扁;腹部有棱鱗,沿近海表層洄游性中小型魚類,有時...
一個完全四點形(四線形)實際上含有四點(線)1,2,3,4和它們的六條連線交點23,14,31,24,12,34;其中23與14、31與24、12與34稱為對邊(對頂點)....
密克爾點(Miquel點又譯:米格爾點、密克點或米庫爾點):來自密克爾定理中的完全四邊形定理:如果ABCDEF是完全四邊形,那么三角形△EAD,△EBC,△FAB,△FDC的外接圓交...
1639年笛沙格在其著作中提出了“笛沙格對合定理”,其中列出了“完全四點(線)形”和“四點(線)偶”的概念。笛沙格對合定理指的是通過一個已知四點形的頂點所...
2、過圓外一點作圓的兩條切線與一條割線,與圓相交的四點構成的凸四邊形為調和四邊形。參考資料 1. 完全四點形和完全四線形調和性質套用例析 .百度文庫[引用...
由四條直線(其中無三線共點)以及其中任意兩條直線的六個交點所組成的圖形叫完全四邊形(右圖b)。這四條直線叫邊,六個點叫頂點,不在公共邊上的兩頂點叫對頂,...
表2 n=4,簡單四點形和簡單四線形簡單n線形相關概念 編輯 簡單n線形完全n點形和完全n線形 完全n點形 n個點(其中無三點共線)及其每二點連線所構成的圖形...
(完全四邊形的密克定理) 四條兩兩相交的直線形成四個三角形,它們的外接圓共點 [2] 。米奎爾定理推論2 在△ABC中,點D、E、F分別在邊BC、CA、AB上,設M為其...
