笛沙格對合定理

1639年笛沙格在其著作中提出了“笛沙格對合定理”，其中列出了“完全四點(線)形”和“四點(線)偶”的概念。笛沙格對合定理指的是通過一個已知四點形的頂點所作的二次曲線束與不通過任何一個頂點的直線相交成一對合，其中以同一條二次曲線與該直線的交點為對合對應點。

基本介紹

• 中文名：笛沙格對合定理
• 外文名：Desargues' Involution Theorem
• 所屬學科：射影集合
• 提出者：笛沙格
• 提出時間：1639年
• 提出者國籍：法國

笛沙格對合定理

通過一個已知四點形的頂點所作的二次曲線束與不通過任何一個頂點的直線相交成一對合，其中以同一條二次曲線與該直線的交點為對合對應點。

笛沙格對合定理的證明

設

和

為通過四個已知點的兩條二次曲線。作二次曲線束方程

不失一般性，考慮直線 與二次曲線束的交點，將代入二次曲線束方程得到

這是的二次方程，設和為該方程的兩個根，則

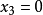
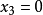
從上式中消去得到

這是關於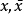的對稱雙線性方程，式中和的係數相等，所以對合。

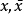
在二次曲線束中，對於每一個確定的所對應的二次曲線與直線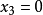相交於屬於一個對合的一對對應點。