密克爾點

密克爾點（Miquel point又譯：米格爾點、密克點或米庫爾點）：來自密克爾定理中的完全四邊形定理：如果ABCDEF是完全四邊形，那么三角形△EAD,△EBC,△FAB,△FDC的外接圓交於一點G，稱為密克爾點。

證明

如右圖，記⊙CBE與⊙CDF的交點為G過G點對AE,CE,CF,AF作垂線，垂足記為P,Q,R,S

由西姆松定理

∵G在⊙CBE上

∴P,Q,R三點共線

∵G在⊙CDF上

∴Q,R,S三點共線

∴P,Q,R,S四點共線

∴G在⊙ADE,⊙ABF上

即G在⊙ADE,⊙ABF,⊙CBE,⊙CDF上

∴四圓共點

密克爾定理

密克爾定理是幾何學中關於相交圓的定理。1838年，奧古斯特·密克敘述並證明了數條相關定理。許多有用的定理可由其推出。

定理陳述

三圓定理：設三個圓C1, C2,C3交於一點O，而M,N,P分別是C1和C2，C2和C3，C3和C1的另一交點。設A為C1的點，直線MA交C2於B，直線PA交C3於C。那么B,N , C這三點共線。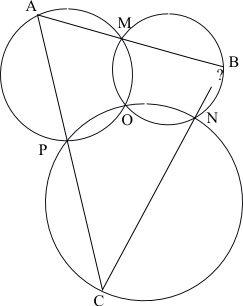

逆定理：如果有一△ABC，M,N,P三點分別在邊AB,BC,CA上，那么△AMP, △BMN, △CNP的外接圓交於一點O。

四圓定理：設C1，C2，C3，C4為四個圓，A1和B1是C1和C2的交點，A2和B2是C2和C3的交點，A3和B3是C3和C4的交點，A4和B4是C1和C4的交點。那么A1，A2，A3，A4四點共圓若且唯若B1，B2，B3，B4四點共圓。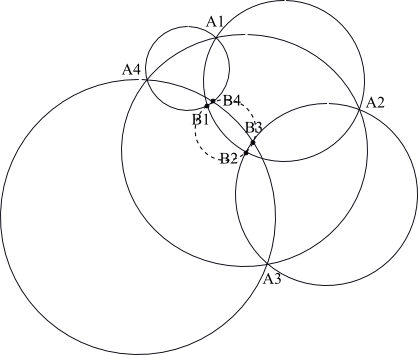

五圓定理：設ABCDE為任意五邊形，五點F,G,H,I,J分別是EA和BC, AB和CD, BC和DE, CD和EA, DE和AB的交點，那么三角形△ABF, △BCG, △CDH, △DEI, △EAJ的外接圓的五個不在五邊形上的交點共圓，而且穿過這些交點的圓也穿過五個外接圓的圓心。

逆定理：設C1，C2，C3，C4，C5五個圓的圓心都在圓C上，相鄰的圓交於C上，那么把它們不在C上的交點與比鄰同樣的點連起來，所成的五條直線相交於這五個圓上。

1838年奧古斯特·密克在約瑟夫·劉維爾的期刊《Journal de mathématiques pures et appliquées》（純粹與套用數學雜誌）發表了這定理的一部份。

密克的第一條定理，是很久前已有的著名經典結果，以圓周角定理證明。

完全四線形四圓的交點現在稱為密克爾點，但這性質雅各布·施泰納在1828年已經知道，威廉·華萊士也很可能已經知道。