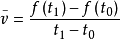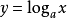歷史沿革 起源 大約在1629年,法國數學家
費馬 研究了作曲線的切線和求函式
極值 的方法;1637年左右,他寫一篇手稿《求最大值與最小值的方法》。在作切線時,他構造了
差分 f(A+E)-f(A),發現的因子E就是我們所說的導數f'(A)。
發展 17世紀生產力的發展推動了自然科學和技術的發展,在前人創造性研究的基礎上,大數學家
牛頓 、
萊布尼茨 等從不同的角度開始系統地研究微積分。牛頓的微積分理論被稱為“流數術”,他稱變數為流量,稱變數的變化率為
流數 ,相當於我們所說的導數。牛頓的有關“流數術”的主要著作是《求曲邊形面積》、《運用無窮多項方程的計算法》和《流數術和
無窮級數 》,流數理論的實質概括為:他的重點在於一個變數的函式而不在於多變數的方程;在於自變數的變化與函式的變化的比的構成;最在於決定這個比當變化趨於零時的極限。
成熟 1750年
達朗貝爾 在為法國科學家院出版的《
百科全書 》第四版寫的“微分”條目中提出了關於導數的一種觀點,可以用現代符號簡單表示:
。
1823年,
柯西 在他的《無窮小分析概論》中定義導數:如果函式y=f(x)在變數x的兩個給定的界限之間保持連續,並且我們為這樣的變數指定一個包含在這兩個不同界限之間的值,那么是使變數得到一個無窮小增量。19世紀60年代以後,
魏爾斯特拉斯 創造了ε-δ語言,對微積分中出現的各種類型的極限重加表達。
微積分學理論基礎,大體可以分為兩個部分。一個是
實無限 理論,即無限是一個具體的東西,一種真實的存在;另一種是
潛無限 理論,指一種意識形態上的過程,比如無限接近。
就數學歷史來看,兩種理論都有一定的道理,實無限就使用了150年。
光是電磁波還是粒子是一個物理學長期爭論的問題,後來由波粒二象性來統一。微積分無論是用現代極限論還是150年前的理論,都不是最好的方法。
定義 設
函式 y=f(x)在點x
0 的某個
鄰域 內有定義,當自變數x在x
0 處有增量Δx,(x
0 +Δx)也在該鄰域內時,相應地函式取得
增量 Δy=f(x
0 +Δx)-f(x
0 );如果Δy與Δx之比當Δx→0時
極限 存在,則稱函式y=f(x)在點x
0 處可導,並稱這個極限為函式y=f(x)在點x
0 處的導數記作
① ;
② ;
③ , 即
需要指出的是:
兩者在數學上是等價的。
導函式 如果函式y=f(x)在開區間內每一點都可導,就稱函式f(x)在區間內可導。這時函式y=f(x)對於區間內的每一個確定的x值,都對應著一個確定的導數值,這就構成一個新的函式,稱這個函式為原來函式y=f(x)的
導函式 ,記作y'、f'(x)、dy/dx或df(x)/dx,簡稱導數。
導數是微積分的一個重要的支柱。
牛頓 及
萊布尼茨 對此做出了貢獻。
幾何意義 函式y=f(x)在x0 點的導數f'(x0 )的幾何意義:表示函式曲線在點P0 (x0 ,f(x0 ))處的切線的斜率(導數的幾何意義是該函式曲線在這一點上的切線斜率)。
公式 簡單函式 複雜函式 1、導數的四則運算:
高階導數運算法則 y=f(x)的反函式是x=g(y),則有y'=1/x'。
複合函式對自變數的導數,等於已知函式對中間變數的導數,乘以中間變數對自變數的導數(稱為
鏈式法則 )。
4、變限積分的求導法則:
(a(x),b(x)為子函式)
導數的計算 計算已知函式的導函式可以按照導數的定義運用變化比值的極限來計算。在實際計算中,大部分常見的解析函式都可以看作是一些簡單的函式的和、差、積、商或相互複合的結果。只要知道了這些簡單函式的導函式,那么根據導數的求導法則,就可以推算出較為複雜的函式的導函式。
導數的求導法則 由基本函式的和、差、積、商或相互複合構成的函式的導函式則可以通過函式的求導法則來推導。基本的求導法則如下:
1、求導的線性:對函式的線性組合求導,等於先對其中每個部分求導後再取線性組合(即①式)。
2、兩個函式的乘積的導函式:一導乘二+一乘二導(即②式)。
3、兩個函式的商的導函式也是一個分式:(子導乘母-子乘母導)除以母平方(即③式)。
4、如果有複合函式,則用鏈式法則求導。
高階求導 1、直接法:由高階導數的定義逐步求高階導數。
一般用來尋找解題方法。
3、間接法:利用已知的高階導數公式,通過
四則運算 ,變數代換等方法。
注意:代換後函式要便於求,儘量
靠攏 已知公式求出階導數。
口訣 為了便於記憶,有人整理出了以下口訣:
常為零, 冪降次
對倒數( e 為底時直接倒數,a為底時乘以1/lna)
指不變( 特別的,自然對數的指數函式完全不變,一般的指數函式須乘以lna)
正變余,余變正
切割方( 切函式是相應割函式(切函式的倒數)的平方)
割乘切,反分式
導數與函式的性質 單調性 (1)若導數大於零,則單調遞增;若導數小於零,則單調遞減;導數等於零為函式
駐點 ,不一定為
極值點 。需代入駐點左右兩邊的數值求導數正負判斷單調性。
(2)若已知函式為遞增函式,則導數大於等於零;若已知函式為遞減函式,則導數小於等於零。
如果函式的導函式在某一區間內恆大於零(或恆小於零),那么函式在這一區間內單調遞增(或單調遞減),這種區間也稱為函式的單調區間。導函式等於零的點稱為函式的駐點,在這類點上函式可能會取得極大值或極小值(即極值可疑點)。進一步判斷則需要知道導函式在附近的符號。對於滿足的一點,如果存在使得在之前區間上都大於等於零,而在之後區間上都小於等於零,那么是一個極大值點,反之則為極小值點。
x變化時函式(藍色曲線)的切線變化。函式的導數值就是切線的斜率,綠色代表其值為正,紅色代表其值為負,黑色代表值為零。
凹凸性 可導函式的凹凸性與其導數的單調性有關。如果函式的導函式在某個區間上單調遞增,那么這個區間上函式是向下凹的,反之則是向上凸的。如果二階導函式存在,也可以用它的正負性判斷,如果在某個區間上恆大於零,則這個區間上函式是向下凹的,反之這個區間上函式是向上凸的。曲線的凹凸分界點稱為曲線的
拐點 。
導數種別 雙曲函式 另外在對
雙曲函式 shx,chx,thx等以及反雙曲函式arshx,archx,arthx等和其他較複雜的複合函式求導時通過查閱
導數表 和運用開頭的公式與
均能較快捷地求得結果。
冪函式 導數說白了它其實就是曲線一點切線的斜率,函式值的變化率。
上面說的分母趨於零,這是當然的了,但不要忘了分子也是可能趨於零的,所以兩者的比就有可能是某一個數,如果分子趨於某一個數,而不是零的話,那么比值會很大,可以認為是
無窮大 ,也就是我們所說的導數不存在。
設y=x/x,若這裡讓x趨於零的話,分母是趨於零了,但它們的比值是1,所以極限為1。
連續不可導的曲線 例如,
魏爾斯特拉斯函式 (Weierstrass function)就是一類處處連續而處處不
可導 的實值函式。魏爾斯特拉斯函式是一種無法用筆畫出任何一部分的函式,因為每一點的導數都不存在,畫的人無法知道每一點該朝哪個方向畫。魏爾斯特拉斯函式的每一點的
斜率 也是不存在的。魏爾斯特拉斯函式得名於十九世紀的德國數學家
卡爾·魏爾斯特拉斯 (Karl Theodor Wilhelm Weierstrass,1815–1897)。歷史上,魏爾斯特拉斯函式是一個著名的數學反例。魏爾斯特拉斯之前,數學家們對函式的連續性認識並不深刻。許多數學家認為除了少數一些特殊的點以外,連續的函式曲線在每一點上總會有斜率。魏爾斯特拉斯函式的出現說明了所謂的“病態”函式的存在性,改變了當時數學家對連續函式的看法。
套用 導數與物理,幾何,代數關係密切:在幾何中可求
切線 ;在代數中可求瞬時變化率;在物理中可求速度、加速度。
導數亦名紀數、
微商 (
微分 中的概念),是由速度變化問題和曲線的切線問題(矢量速度的方向)而抽象出來的數學概念,又稱變化率。
如一輛汽車在10小時內走了 600千米,它的平均速度是60千米/小時。但在實際行駛過程中,是有快慢變化的,不都是60千米/小時。為了較好地反映汽車在行駛過程中的快慢變化情況,可以縮短時間間隔,設汽車所在位置s與時間t的關係為:
那么汽車在由時刻t
0 變到t
1 這段時間內的平均速度是:
當 t
1 無限趨近於t
0 時,汽車行駛的快慢變化就不會很大,平均速度就近似等於t
0 時刻的瞬時速度,因而就把此時的
極限 作為汽車在時刻t
0 的瞬時速度,即
,這就是通常所說的速度。這實際上是由平均速度
類比 到瞬時速度的過程 (如我們駕駛時的限“速” 指瞬時速度)。
導數另一個定義:當x=x0 時,f'(x0 )是一個確定的數。這樣,當x變化時,f'(x)便是x的一個函式,我們稱他為f(x)(關於x)的導函式(derivative function),簡稱導數。
物理學、幾何學、經濟學等學科中的一些重要概念都可以用導數來表示。如:導數可以表示運動物體的瞬時速度和加速度(就直線運動而言,位移關於時間的
一階導數 是瞬時速度,
二階導數 是加速度),可以表示曲線在一點的
斜率 ,還可以表示經濟學中的邊際和彈性。
以上說的經典導數定義可以認為是反映局部
歐氏空間 的函式變化。為了研究更一般的
流形 上的
向量叢 截面 (比如
切向量場 )的變化,導數的概念被推廣為所謂的“聯絡”。有了聯絡,人們就可以研究大範圍的幾何問題,這是微分幾何與物理中最重要的基礎概念之一。
注意:
2、導數為零的點不一定是
極值 點。當函式為
常值函式 ,沒有增減性,即沒有
極值點 。但導數為零。(導數為零的點稱之為駐點,如果駐點兩側的導數的符號相反,則該點為極值點,否則為一般的駐點,如
中f'(0)=0,x=0的左右導數符號為正,該點為一般駐點。)
求導方法(定義法):
②求平均變化率;
③取極限,得導數。





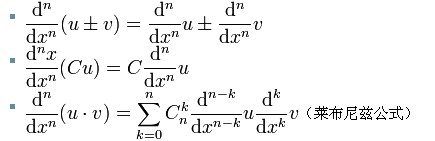 高階導數運算法則
高階導數運算法則