增量亦稱改變數,指的是在一段時間內,自變數取不同的值所對應的函式值之差。
基本介紹
- 中文名:增量
- 外文名:increment
- 所屬學科:數學
- 定義:自變數取不同值對應的函式值之差
- 別名:改變數
定義

常見函式模型

 圖1
圖1
 圖3
圖3
 圖4
圖4
 圖5
圖5
 圖6
圖6 圖7
圖7







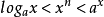

增量亦稱改變數,指的是在一段時間內,自變數取不同的值所對應的函式值之差。


 圖1
圖1
 圖3
圖3
 圖4
圖4
 圖5
圖5
 圖6
圖6 圖7
圖7







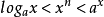
增量亦稱改變數,指的是在一段時間內,自變數取不同的值所對應的函式值之差。...... 增量亦稱改變數,指的是在一段時間內,自變數取不同的值所對應的函式值之差...
增量更新是指在進行更新操作時,只更新需要改變的地方,不需要更新或者已經更新過的地方則不會重複更新,增量更新與完全更新相對。這種更新的概念套用範圍比較廣泛,凡是...
增量,是強調軟體在發布不同的版本時,每次都多發布一點點,是軟體功能數量漸增地發布的過程。...
增量式編碼器是將位移轉換成周期性的電信號,再把這個電信號轉變成計數脈衝,用脈衝的個數表示位移的大小,按照工作原理編碼器可分為增量式和絕對式兩類。...
增量學習是指一個學習系統能不斷地從新樣本中學習新的知識,並能保存大部分以前已經學習到的知識。增量學習非常類似於人類自身的學習模式。因為人在成長過程中,每天...
資本增量是指企業在資本存量基礎上增加的資本投入量,它一方面表現為企業資產的增加,另一方面也表現為企業權益(負債或所有者權益)的增加。...
增量調整是指根據國家的產業政策和技術政策,通過對投資方向的改變,把資金投向重點建設項目和重點技術改造項目,促使產業結構合理化,達到資源的最佳化組合,提高經濟效益。....
增量備份(incremental backup)是備份的一個類型,是指在一次全備份或上一次增量備份後,以後每次的備份只需備份與前一次相比增加或者被修改的檔案。...
增量模型是把待開發的軟體系統模組化,將每個模組作為一個增量組件,從而分批次地分析、設計、編碼和測試這些增量組件。運用增量模型的軟體開發過程是遞增式的過程。...
與“記憶體增量”同義,為Windows系統任務管理器,進程頁面,顯示項其中之一,默認不顯示,需用戶手動選擇列調出。...
希爾排序Shellsort是指希爾提出了一種衝破二次時間屏障的算法,希爾增量是希爾排序中希爾給出的增量序列ht = N / 2, h[k] = h[k+1] / 2,即{N/2, (N...
增量最佳化是指在增加企業資產總量的基礎上來最佳化企業的資本結構。...... 增量最佳化是指在增加企業資產總量的基礎上來最佳化企業的資本結構。增量最佳化的途徑...
所謂增量改革,按照中國人民大學經濟學院院長楊瑞龍的觀點,就是借用等級規則確立產權規則,政府導向式改革的優點非常明顯,其在傳統體制上的邊際效益大大減少了改革阻力,...
兩點平面直角坐標值之差值,即橫縱坐標的增加值,稱為坐標增量。...... 兩點平面直角坐標值之差值,即橫縱坐標的增加值,稱為坐標增量。中文名 坐標增量 外文名 ...
增量理論指的是由於材料在進入塑性狀態時的非線性性質和塑性變形的不可恢復的特點,因此須研究應力增量和應變增量之間的關係。...
增量資金:指在這個資本市場本體內增加的資金。例如:儲蓄錢、險資、養老基金等新進資金都可被統稱為增量資金。...
存量增量是指企業或社會所擁有的全部可確指的資產或資源以及比期初增加的資產或資源。...
增量法是根據企業產品推銷任務量的增加或產品銷售區域的擴大,逐步地增加推銷人員的方法。但產品推銷任務量的增加或產品銷售區域的擴大,與推銷人員數量上的增加不一定...
增量成本指為建設某一項目而增加的國民經濟代價。在國民經濟效益評價中,由於建設某一項目而使國民經濟失去的各種資源,是項目建設和生產過程中國民經濟所增加的耗費。...
增量信息編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 增量信息 英文名稱 incremental information 定義 ...
增量式開發,又叫增量開發,是軟體工程當中,一種常用的軟體開發過程思想。其中增量是指在軟體開發過程中,先開發主要功能模組,再開發次要功能模組,逐步完善,最終開發...
增量分析法,是指對被比較方案在成本、收益等方面的差額部分進行分析,進而對方案進行比較、選優的方法。增量分析法的具體分析過程所採用的方法是剔除法,即對所有備...
增量編碼器輸出脈衝信號,集電極開路,長線驅動,推挽,互補,絕對值信號輸出有:SSI、4-20MA、profibus-dp、DEVicenet、並行、二進制碼、、BiSS、ISI、CANopen、Endat及...
增量投資內部收益率(The Incremental IRR Rule)△IRR是兩個方案各年淨現金流量的差額的現值之和等於零時的折現率。...
