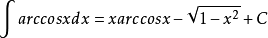基本介紹
- 中文名:反三角函式
- 外文名:Inverse trigonometric function
- 分類:反正弦、反餘弦、反正切等
- 函式等級:初等函式
- 一級學科:數學、理學
- 二級學科:平面三角
簡介,分類,反正弦函式,反餘弦函式,反正切函式,反餘切函式,反正割函式,反餘割函式,公式,餘角關係,負數關係,倒數關係,三角函式關係,加減法公式,級數定義,導數,不定積分,
簡介
反三角函式(inverse trigonometric function)是一類初等函式。指三角函式的反函式。由於基本三角函式具有周期性,所以反三角函式是多值函式。這種多值的反三角函式包括:反正弦函式、反餘弦函式、反正切函式、反餘切函式、反正割函式、反餘割函式,分別記為Arcsin x,Arccos x,Arctan x,Arccot x,Arcsec x,Arccsc x。但是,在實函式中一般只研究單值函式,只把定義在包含銳角的單調區間上的基本三角函式的反函式,稱為反三角函式,這是亦稱反圓函式。為了得到單值對應的反三角函式,人們把全體實數分成許多區間,使每個區間內的每個有定義的 y 值都只能有惟一確定的 x 值與之對應。為了使單值的反三角函式所確定區間具有代表性,常遵循如下條件:
1、為了保證函式與自變數之間的單值對應,確定的區間必須具有單調性;
2、函式在這個區間最好是連續的(這裡之所以說最好,是因為反正割和反餘割函式是尖端的);
3、為了使研究方便,常要求所選擇的區間包含0到π/2的角;
4、所確定的區間上的函式值域應與整函式的定義域相同。這樣確定的反三角函式就是單值的,為了與上面多值的反三角函式相區別,在記法上常將Arc中的A改記為a,例如單值的反正弦函式記為arcsin x。
分類
為限制反三角函式為單值函式,將反正弦函式的值y限在-π/2≤y≤π/2,將y作為反正弦函式的主值,記為y=arcsin x;相應地,反餘弦函式y=arccos x的主值限在0≤y≤π;反正切函式y=arctan x的主值限在-π/2<y<π/2;反餘切函式y=arccot x的主值限在0<y<π。
反正弦函式
正弦函式y=sin x在[-π/2,π/2]上的反函式,叫做反正弦函式。記作arcsinx,表示一個正弦值為x的角,該角的範圍在[-π/2,π/2]區間內。定義域[-1,1] ,值域[-π/2,π/2]。
反餘弦函式
餘弦函式y=cos x在[0,π]上的反函式,叫做反餘弦函式。記作arccosx,表示一個餘弦值為x的角,該角的範圍在[0,π]區間內。定義域[-1,1] , 值域[0,π]。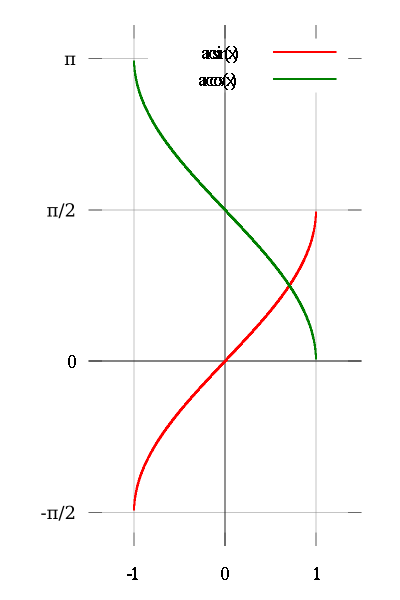 綠的為y=arccos(x) 紅的為y=arcsin(x)
綠的為y=arccos(x) 紅的為y=arcsin(x)
 綠的為y=arccos(x) 紅的為y=arcsin(x)
綠的為y=arccos(x) 紅的為y=arcsin(x)反正切函式
正切函式y=tan x在(-π/2,π/2)上的反函式,叫做反正切函式。記作arctanx,表示一個正切值為x的角,該角的範圍在(-π/2,π/2)區間內。定義域R,值域(-π/2,π/2)。
反餘切函式
餘切函式y=cot x在(0,π)上的反函式,叫做反餘切函式。記作arccotx,表示一個餘切值為x的角,該角的範圍在(0,π)區間內。定義域R,值域(0,π)。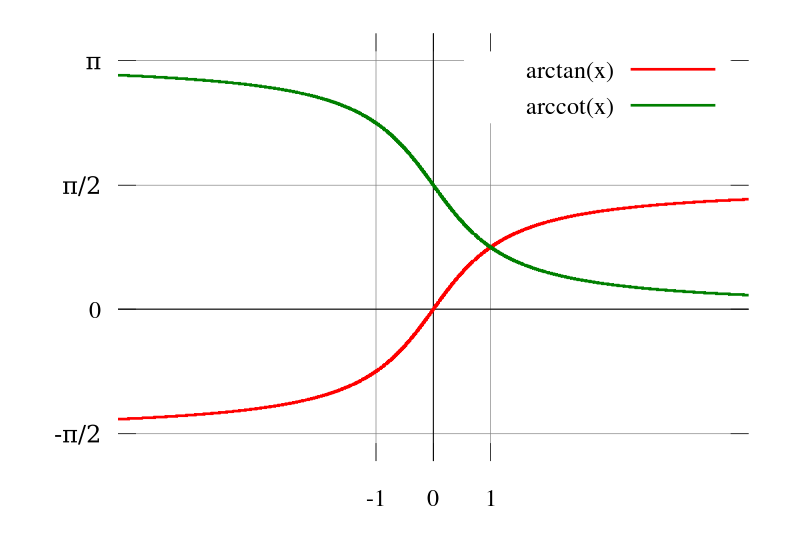 綠的為y=arccot(x) 紅的為y=arctan(x)
綠的為y=arccot(x) 紅的為y=arctan(x)
 綠的為y=arccot(x) 紅的為y=arctan(x)
綠的為y=arccot(x) 紅的為y=arctan(x)反正割函式
正割函式y=sec x在[0,π/2)U(π/2,π]上的反函式,叫做反正割函式。記作arcsecx,表示一個正割值為x的角,該角的範圍在[0,π/2)U(π/2,π]區間內。定義域(-∞,-1]U[1,+∞),值域[0,π/2)U(π/2,π]。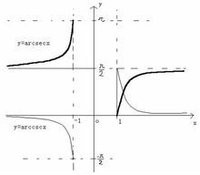 反正割函式
反正割函式
 反正割函式
反正割函式反餘割函式
餘割函式y=csc x在[-π/2,0)U(0,π/2]上的反函式,叫做反餘割函式。記作arccscx,表示一個餘割值為x的角,該角的範圍在[-π/2,0)U(0,π/2]區間內。定義域(-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。
公式
餘角關係



負數關係



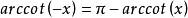


倒數關係


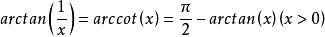




三角函式關係
 |  |  | |
 |  |  | |
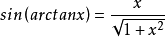 |  |  | |
 |  |  | |
 |  | 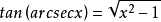 | |
 |  |  |
加減法公式
(1)arcsinx+arcsiny



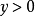




(2)arcsinx-arcsiny






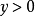

(3)arccosx+arccosy



(4)arccosx-arccosy


(5)arctanx+arctany



(6)arctanx-arctany


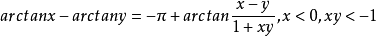
(7)arccotx+arccoty


級數定義



導數


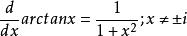
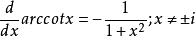
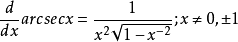

不定積分