基本介紹
發展歷史
定義
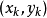
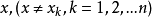
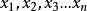
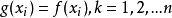
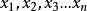
主要內涵
基本類型
多項式
埃爾米特
分段
三角函式
編程使用
插值方法 | 說明 |
nearest | 臨近的兩點插值 |
linear | 線性插值(默認) |
spline | 三次樣條插值 |
pchip | 分段三次Hermite插值多項式插值 |
cubic | (作用於pchip相同) |
v5cubic | 用matlab5版本中斷三次樣條插值 |

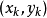
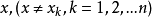
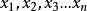
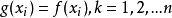
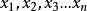
插值方法 | 說明 |
nearest | 臨近的兩點插值 |
linear | 線性插值(默認) |
spline | 三次樣條插值 |
pchip | 分段三次Hermite插值多項式插值 |
cubic | (作用於pchip相同) |
v5cubic | 用matlab5版本中斷三次樣條插值 |
在離散數據的基礎上補插連續函式,使得這條連續曲線通過全部給定的離散數據點。插值是離散函式逼近的重要方法,利用它可通過函式在有限個點處的取值狀況,估算出函式在...
插值法又稱“內插法”,是利用函式f (x)在某區間中已知的若干點的函式值,作出適當的特定函式,在區間的其他點上用這特定函式的值作為函式f (x)的近似值,這種...
空間插值常用於將離散點的測量數據轉換為連續的數據曲面,以便與其它空間現象的分布模式進行比較,它包括了空間內插和外推兩種算法。空間內插算法:通過已知點的數據...
線性插值是指插值函式為一次多項式的插值方式,其在插值節點上的插值誤差為零。線性插值相比其他插值方式,如拋物線插值,具有簡單、方便的特點。線性插值的幾何意義即為...
圖像插值就是利用已知鄰近像素點的灰度值(或rgb圖像中的三色值)來產生未知像素點的灰度值,以便由原始圖像再生出具有更高解析度的圖像。...
圖像插值是在基於模型框架下,從低解析度圖像生成高解析度圖像的過程,用以恢復圖像中所丟失的信息。圖象插值方法有:最近鄰插值,雙線性插值,雙平方插值,雙立方插值以及...
設函式f的離散數據為(xi,yi),yi=f(xi),i=0,1,2,...,n,插值的目的是在x0,x1,x2,...,xn之間給定了自變數x的值後,要去求函式f的近似值,其途徑是...
三次插值法(cubic interpolation method)是一種多項式插值法,逐次以三次曲線φ(t)=a0+a1t+a2t2+a3t3的極小點逼近尋求函式f(t)的極小點的一種方法.具體做法...
三次樣條插值(Cubic Spline Interpolation)簡稱Spline插值,是通過一系列形值點的一條光滑曲線,數學上通過求解三彎矩方程組得出曲線函式組的過程。實際計算時還需要...
雙三次插值,英文是Bicubic interpolation。雙三次插值是一種更加複雜的插值方式,它能創造出比雙線性插值更平滑的圖像邊緣。雙三次插值方法通常運用在一部分圖像處理...
IDW(Inverse Distance Weighted)是一種常用而簡便的空間插值方法,它以插值點與樣本點間的距離為權重進行加權平均,離插值點越近的樣本點賦予的權重越大。 設平面上...
插值法又稱“內插法”,是利用函式f (x)在某區間中已知的若干點的函式值,作出適當的特定函式,在區間的其他點上用這特定函式的值作為函式f (x)的近似值,這種...
插值(Interpolation),是一種為數位相機在計算像素時可以增加有效像素(實際像素)的成像方式。...
雙線性插值,又稱為雙線性內插。在數學上,雙線性插值是有兩個變數的插值函式的線性插值擴展,其核心思想是在兩個方向分別進行一次線性插值。雙線性插值作為數值分析...
最臨近插值,通常被用於圖像縮放中,進行縮放圖像的方法叫做最臨近插值算法,這是一種最基本、最簡單的圖像縮放算法。效果並不好,放大後的圖像有很嚴重的馬賽克,縮小...
克里金(Kriging)插值法,又稱空間自協方差最佳插值法,它是以南非礦業工程師D.G.Krige的名字命名的一種最優內插法。克里金法廣泛地套用於地下水模擬、土壤製圖等...
指數插值(exponential interpolation)是常用的插值方法之一,指用指數函式之和作為插值函式的插值方法。例如,在分析放射性元素衰減時常被採用。...
拋物插值(parabolic interpolation)一種插值方法.指以二次多項式為插值函式的插值方法...
埃爾米特插值公式(Hermite interpolation formina )區域上解析函式的拉格朗日插值多項式的積分表示式。不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應...
在數值分析中,拉格朗日插值法是以法國十八世紀數學家約瑟夫·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函式來表示某種內在聯繫或規律,而不少函式都只能...
最優插值法( 又稱統計內插)是從統計意義上來說均方差最小的線性插值方法。它以線性最小平方估計理論為基礎,其優點是能夠“自動”地處理精度不同的各種觀測數據,...
插值序列是單位圓內滿足某種函式論條件的點列。1958年,卡爾松(Carleson,L.)證明了{zk}是插值序列的充分必要條件是:{zk}是均勻分散的。...
拉格朗日插值公式(外文名Lagrange interpolation formula)指的是在節點上給出節點基函式,然後做基函式的線性組合,組合係數為節點函式值的一種插值多項式。...
又稱插值法。根據未知函式f(x)在某區間內若干點的函式值,作出在該若干點的函式值與f(x)值相等的特定函式來近似原函式f(x),進而可用此特定函式算出該區間內...
