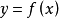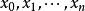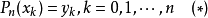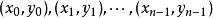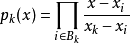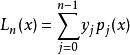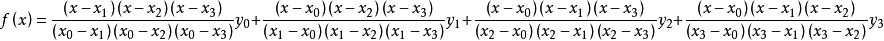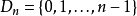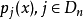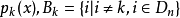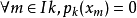拉格朗日插值法

在數值分析中，拉格朗日插值法是以法國十八世紀數學家約瑟夫·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函式來表示某種內在聯繫或規律，而不少函式都只能通過實驗和觀測來了解。如對實踐中的某個物理量進行觀測，在若干個不同的地方得到相應的觀測值，拉格朗日插值法可以找到一個多項式，其恰好在各個觀測的點取到觀測到的值。這樣的多項式稱為拉格朗日（插值）多項式。數學上來說，拉格朗日插值法可以給出一個恰好穿過二維平面上若干個已知點的多項式函式。拉格朗日插值法最早被英國數學家愛德華·華林於1779年發現，不久後（1783年）由萊昂哈德·歐拉再次發現。1795年，拉格朗日在其著作《師範學校數學基礎教程》中發表了這個插值方法，從此他的名字就和這個方法聯繫在一起。

基本介紹

• 中文名：拉格朗日插值法
• 外文名：Lagrange Interpolation Polynomial
• 領域：數值分析
• 地區：法國
• 時代：十八世紀
• 作者：拉格朗日

發現歷程

在數值分析中，拉格朗日插值法是以法國十八世紀數學家約瑟夫·路易斯·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函式來表示某種內在聯繫或規律，而不少函式都只能通過實驗和觀測來了解。如對實踐中的某個物理量進行觀測，在若干個不同的地方得到相應的觀測值，拉格朗日插值法可以找到一個多項式，其恰好在各個觀測的點取到觀測到的值。這樣的多項式稱為拉格朗日（插值）多項式。數學上來說，拉格朗日插值法可以給出一個恰好穿過二維平面上若干個已知點的多項式函式。拉格朗日插值法最早被英國數學家愛德華·華林於1779年發現，不久後（1783年）由萊昂哈德·歐拉再次發現。1795年，拉格朗日在其著作《師範學校數學基礎教程》中發表了這個插值方法，從此他的名字就和這個方法聯繫在一起。

定義

概念

一般地，若已知 在互不相同 n+1 個點 處的函式值 ( 即該函式過 這n+1個點），則可以考慮構造一個過這n+1 個點的、次數不超過n的多項式 ,使其滿足：

要估計任一點ξ，ξ≠x_i,i=0,1,2,...,n,則可以用P_n（ξ）的值作為準確值f(ξ)的近似值，此方法叫做“插值法”。

稱式（*）為插值條件（準則），含x_i(i=0,1,...,n)的最小區間[a,b]，其中a=min{x₀,x₁,...,x_n}，b=max{x₀,x₁,...,x_n}。

定理

滿足插值條件的、次數不超過n的多項式是存在而且是唯一的。

一般形式運用方法

在平面上有 共n個點，現作一條函式 使其圖像經過這n個點。

作法：設集合是關於點的角標的集合，，作n個多項式 。對於任意，都有

使得

是n-1次多項式，且滿足並且。

最後可得。

形如上式的插值多項式稱為拉格朗日（Lagrange）插值多項式。

例如：當n=4時，上面的公式可簡化為：

這是一個過4個點的唯一的三次多項式。