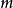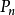雷米茲算法,或稱雷米茲交換算法,由葉夫根尼·列維奇·雷米茲於1934年所發表。 雷米茲算法為一尋找函式簡易近似之疊代算法,特別是定義於切比雪夫空間的函式效果最佳。
一個在切比雪夫空間的典型例子是 n 次項切比雪夫多項式的子空間,屬於實數連續函式之向量空間,定義於 C[a, b] 區間。
給定一子空間,其最佳近似多項式的定義為:可將此近似多項式與原始函式之最大絕對差異最小化者。 在這個情況下,可由equioscillation theorem使其解更精確.
基本介紹
- 中文名:雷米茲演算法
- 外文名:Remez algorithm
- 分類:數理科學
程式,初始化選擇,細節討論,變異,
程式
- 解線性系統之等式


對於未知的 及E。
及E。

使用 作為多項式
作為多項式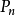 的係數。
的係數。

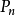
找出集合M,為 之區域極大錯誤點。
之區域極大錯誤點。

此結果稱為最佳近似多項式、切比雪夫近似、或最小化最大近似。
初始化選擇
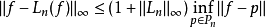

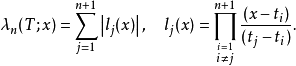
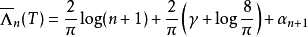


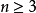
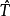

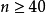

細節討論
在此將提供先前簡述步驟的詳細內容,在這個章節令指數i從 0 跑到n+1.
步驟 1:給定 , 求n+2 條等式之線性系統之解


對於未知的 和E.
和E.

可以很清楚地觀察到,在這個式子裡 若要成立,只有在節點
若要成立,只有在節點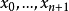 為排序的情況下才能達到,無論是嚴格遞增或遞減。這樣一來這個線性系統便有唯一解。(廣為人知的,並非每個線性系統都可以求解)。 此外,求解之複雜度最少為
為排序的情況下才能達到,無論是嚴格遞增或遞減。這樣一來這個線性系統便有唯一解。(廣為人知的,並非每個線性系統都可以求解)。 此外,求解之複雜度最少為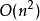 ,而一個從函式庫求解的標準計算器需要
,而一個從函式庫求解的標準計算器需要  的複雜度,在此有一簡單證明:
的複雜度,在此有一簡單證明:

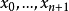
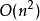

計算前n+1個節點之{\displaystyle f(x)}標準n階插值  , 以及對於{\displaystyle (-1)^{i}}之標準n階插值
, 以及對於{\displaystyle (-1)^{i}}之標準n階插值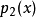

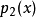
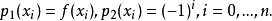

在 與
與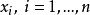 之間,多項式
之間,多項式 有其i-階 零點zero between
有其i-階 零點zero between  ,因此在
,因此在 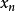 與
與  之間無任何零點,意即
之間無任何零點,意即  與
與  正負號
正負號  相同。
相同。

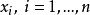


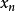




線性組合  亦為一n次多項式
亦為一n次多項式


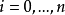
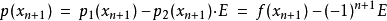
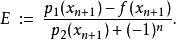
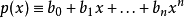
給定n+2 階節點,其誤差為正負輪流:

步驟 2把多項式表示由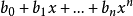 轉為
轉為  .
.
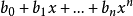

步驟 3依照以下所述改善輸入節點 的誤差{\displaystyle \pm E}。
的誤差{\displaystyle \pm E}。

在每個 P-領域,現在的節點 將被區域最大
將被區域最大 取代,同樣在每個 N-領域,
取代,同樣在每個 N-領域,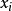 將被區域最小取代, 在這部分並不要求高精確律。
將被區域最小取代, 在這部分並不要求高精確律。


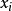
令 , 其大小
, 其大小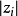 皆大於或等於E。de La Vallée Poussin理論及其證明也可以套用至
皆大於或等於E。de La Vallée Poussin理論及其證明也可以套用至  , 而使此n次多項式有最小可能誤差的新下界為
, 而使此n次多項式有最小可能誤差的新下界為  。
。

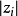


步驟 4:分別以



變異
有時候在最大絕對差異點的附近,會有複數個點同時被取代。
有時候相對誤差會被用來衡量函式與其近似的差異,特別是在電腦上用浮點數做運算的函式。