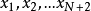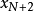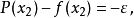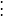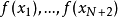數值逼近

簡介

數學中有一個相關性很高的主題，是用廣義傅立葉級數進行函式逼近，也就是用以正交多項式為基礎的級數來進行逼近。

計算機科學中有一個問題和逼近理論有關，就是在數學函式庫中如何用計算機或計算器可以執行的功能（例如乘法和加法）儘可能的逼近某一數學函式，一般會用多項式或有理函式（二多項式的商）來進行。

逼近理論的目標是儘可能的逼近實際的函式，一般精度會接近電腦浮點運算的精度，一般會用高次的多項式，以及（或者）縮小多項式逼近函式的區間。縮小區間可以針對要逼近的函式，利用許多不同的係數及增益來達到。數學函式庫將區間劃分為許多的小區間，每個區間搭配一個次數不高的多項式。

只要選定了多項式的次數及逼近的範圍，就可以用以使最壞情形誤差最小化的原則，來選擇逼近多項式，其目的為最小化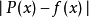

的絕對值，其中P(x)為逼近多項式，而f(x)為實際的函式。對於一個良態的函式，存在一個N次的多項式，使誤差曲線的大小在

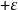和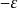

之間震盪至多N+2次，其最壞情形的誤差為

。一個N次的多項式可以內插曲線中的N+1個點。當然也有可能製造一些極端的函式，使得滿足上述條件的多項式不存在，但在實務上很少需要為這様的函式進行逼近。

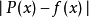
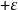
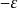
例如右圖中的紅線就是用N=4情形下用多項式逼近log(x)及exp(x)的誤差。誤差在

和

之間震盪。每一個例子中的極端有N+2個，也就是6個。極值出現在區間的端點，也就是圖的最左邊及最右邊。

切比雪夫近似是利用將函式展開為由切比雪夫多項式組成的各項，依需要的逼近程度決定展開的項次，可以得到很接近多項式的結果。此作法類似進行函式的傅立葉分析，只是用切比雪夫多項式代替分析中用到的三角函式。

若計算一函式切比雪夫展開的係數：

只展開到

項為止，可以得到一個逼近f(x)的N次多項式。

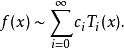
對於一個有快速收斂冪級數的函式而言，若展開到一定項次後截止不再展開，截止產生的誤差接近截止後的第一項，因此誤差可以由截止後的第一項代表。若是用切比雪夫多項式展開，也會有一様的結果。若切比雪夫展開只展開到

，後面截止，其誤差會接近

的整數倍。切比雪夫多項式的特點是在[−1, 1]區間以內．其數值會在+1和−1之間震盪。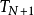

有N+2個極點。因此f(x)和切比雪夫展開的誤差接近一個有N+2個極點的函式，因此為近似最佳的N次多項式。

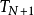
在上面中，可以看到藍色線（切比雪夫近似的誤差）有時比紅色線（最佳多項式的誤差）接近x軸，但有時藍色線反而離x軸較遠，因此切比雪夫近似和最佳多項式畢竟還是有差異。不過exp函式是快速收斂的函式，切比雪夫近似的誤差會比log函式要好。

切比雪夫近似是數值積分方法Clenshaw–Curtis正交法的基礎。

雷米茲算法是在1934年由蘇俄數學家雷米茲提出的算法。可用來產生在一定區間內逼近函式f(x)的最佳多項式P(x)。雷米茲算法是一種疊代式的算法，最後會收斂到使誤差函式N+2個極值的多項式。