基本介紹
- 中文名:牛頓插值公式
- 外文名:Newton interpolation formula
- 提出者:牛頓
- 套用學科:數學,計算力學
差商
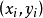
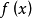
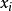

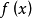
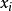

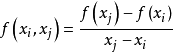
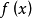
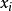



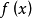


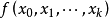

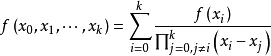
公式推導
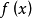

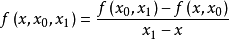

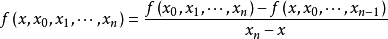

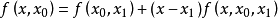

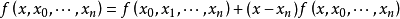
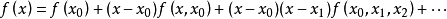
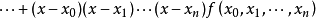
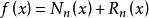
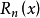
等間距差值公式
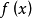
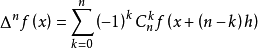

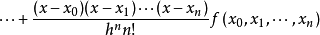
實例
 牛頓插值算例
牛頓插值算例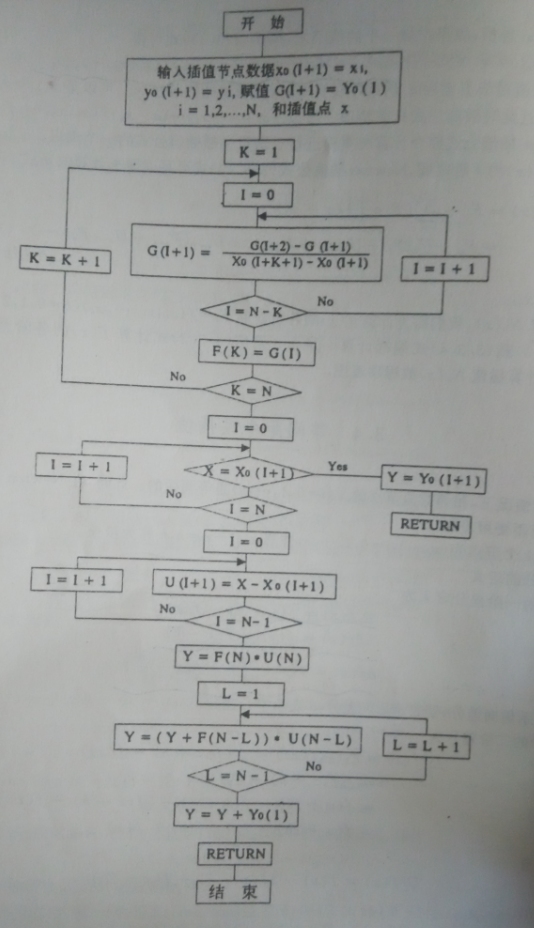
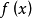
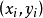
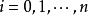
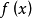
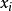

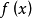
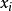

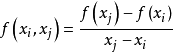
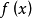
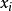



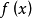


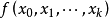

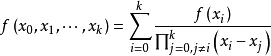
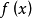

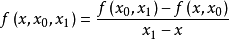

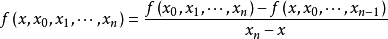

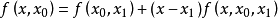

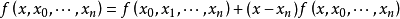
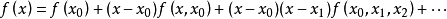
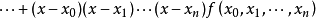
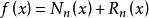
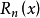
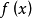
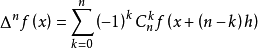

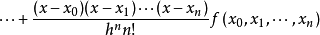
 牛頓插值算例
牛頓插值算例當只知道函式在一些節點的位置卻不知道函式具體的表達式時,我們可以利用代數插值方法給出函式的近似形式。常用的插值公式有拉格朗日插值、牛頓差值、埃米爾特插值及樣條...
插值法利用函式f(x)在某區間中若干點的函式值,作出適當的特定函式,在這些點上取已知值,在區間的其他點上用這特定函式的值作為函式f(x)的近似值。牛頓插值法...
牛頓向後插值公式(Newton backward interpo-lation formula)簡稱牛頓後插公式,是一種等距節點插值公式。特別適用於被插值點二位於插值區間右端點附近的情況。...
張遂一牛頓插值公式(Zhang-Newton interpola-tion formula)亦稱牛頓插值公式一種便於計算的插值多項式,是拉格朗日插值公式的另一種表達形式.具體形式為 依次為零階均...
劉悼一牛頓向前插值公式(Liu-Newton forwardinterpolation formula)亦稱牛頓前插公式一種等距節點插值公式.特別適用於被插值點二位於插值區間左端點附近的情況:二一xo+...
牛頓多項式(英語:Newton Polynomial)是數值分析中一種用於插值的多項式,它以英國數學家和物理學家牛頓命名。...
如果這特定函式是多項式,就稱它為多項式插值。常用的幾種多項式差值法有:直接法、拉格朗日插值法和牛頓插值法。中文名 多項式插值 外文名 polynomial interopolation ...
插值多項式一般有兩種常見的表達形式,一個是拉格朗日插值多項式,另一個是牛頓插值多項式。 [1] 插值埃爾米特 對於函式f(x),常常不僅知道它在一些點的函式值,而且...
插值法Newton插值 編輯 Newton插值也是n次多項式插值,它提出另一種構造插值多項式的方法,與Lagrange插值相比,具有承襲性和易於變動節點的特點。...
設函式f的離散數據為(xi,yi),yi=f(xi),i=0,1,2,...,n,插值的目的是...為節點的牛頓插值多項式 ,用 近似 。反插值反插值及餘項 編輯 假設...
通過選擇Πn,可以簡化係數的計算,但是當用單項式表示內插多項式時,必須進行額外的計算。1、一種方法是以牛頓形式的多項式插值法,並使用分差法來構建係數,例如,...
5?1插值的基本概念5?2拉格朗日插值法5?2?1拉格朗日插值多項式的構造5?2?2插值多項式的餘項5?2?3插值的逼近性質5?3埃特金逐步插值法5?4牛頓插值法...
5.2.1 拉格朗日插值基函式5.2.2 拉格朗日插值及其MATLAB程式5.3 牛頓插值法5.3.1 差商及其性質5.3.2 牛頓插值公式5.3.3 牛頓插值法的MATLAB程式...
6.4牛頓插值多項式6.4.1差商形式的牛頓插值多項式6.4.2差商的基本性質6.4.3差分形式的牛頓插值多項式6.5埃爾米特插值多項式6.5.1構造基函式方法...
13.2 牛頓-拉弗森方法260習題262第14章 插值法26314.1 拉格朗日插值公式26414.1.1 拉格朗日插值多項式26414.1.2 線性插值26614.1.3 二次(拋物線)插值266...
第4章函式插值 4.0概述 4.1牛頓插值 4.1.1一般的牛頓插值 4.1.2等距節點的牛頓插值 4.2拉格朗日插值 4.2.1拉格朗日插值多項式的構造方法 4.2.2插值的誤差估計 4.2...
全書內容共分七章,主要包括緒綸、插值法、函式逼近與曲線擬合、數值微分和數值...6.3 牛頓疊代法 6.4 非線性方程組的解法 習題6 第7章 常微分方程的數值...
3.3 牛頓插值 3.4 Hermite插值 3.5 分段線性插值 3.6 樣條插值 習題 4 曲線擬合 4.1 引言 4.2 曲線擬合的最小二乘法 習題 5 數值積分與數值微分...
計算方法(C語言版)目錄2.5.3簡單疊代法的收斂階262.5.4簡單疊代法的算法和...5.2.6 n 次拉格朗日插值的算法和程式1205.3差商與牛頓插值121...
1 插值法與最小二乘法1.1 插值法1.1.1 概述1.1.2 拉格朗日插值1.1.3 牛頓插值1.1.4 等距節點插值1.1.5 三次樣條插值...
