基本介紹
- 中文名:插值法
- 外文名:interpolation
- 類別:數學
- 別名:內插法
- 分類:Lagrange插值等
- 套用:水質模型等
定義
Lagrange插值
Newton插值
Hermite插值
分段插值
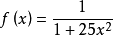
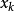
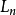

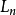
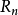
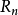




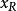


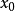

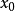



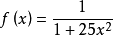
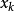
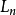

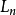
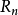
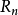




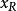





插值法又稱“內插法”,是利用函式f (x)在某區間中已知的若干點的函式值,作出適當的特定函式,在區間的其他點上用這特定函式的值作為函式f (x)的近似值,這種...
線性插值法編輯 鎖定 許多實際問題都用函式y=f(x)來表示內在規律的數量關係,其中相當一部分函式是通過實驗或觀測得到的。雖然f(x)在[a,b]上是存在的,有的...
三次插值法(cubic interpolation method)是一種多項式插值法,逐次以三次曲線φ(t)=a0+a1t+a2t2+a3t3的極小點逼近尋求函式f(t)的極小點的一種方法.具體做法...
在數值分析中,拉格朗日插值法是以法國十八世紀數學家約瑟夫·拉格朗日命名的一種多項式插值方法。許多實際問題中都用函式來表示某種內在聯繫或規律,而不少函式都只能...
樣條插值法是一種以可變樣條來作出一條經過一系列點的光滑曲線的數學方法。插值樣條是由一些多項式組成的,每一個多項式都是由相鄰的兩個數據點決定的,這樣,任意...
插值法利用函式f(x)在某區間中若干點的函式值,作出適當的特定函式,在這些點上取已知值,在區間的其他點上用這特定函式的值作為函式f(x)的近似值。牛頓插值法...
多項式插值法是一種搜尋方法。指用插值多項式φ(t)的極小點逼近尋求函式f(t)的極小點的方法具體做法是:求φ′(t)=0的根,作為f(t)的極小點的近似,重複...
拋物線插值法(parabolic interpolation method)亦稱二次插值法,是一種多項式插值法,逐次以擬合的二次曲線的極小點,逼近原尋求函式極小點的一種方法。具體做法是:設...
插值法是函式逼近的一種重要方法,是數值計算的基本課題。本節只討論具有唯一插值函式的多項式插值和分段多項式插值,對其中的多項式插值主要討論n次多項式插值的方法,即...
最近鄰插值法定義 編輯 最近鄰插值法nearest_neighbor是最簡單的灰度值插值。也稱作零階插值,就是令變換後像素的灰度值等於距它最近的輸入像素的灰度值。...
三次樣條插值法cubic spline inter}x}lalic}i}樣條函式中最重要的一種函式。若函式S(二)在區間【。。川的每一分段}x』一,,二,](i=2,3, } ,n)上是...
雙曲插值法(hyperbolic interpolation method)亦稱線性分式插值法.指用雙曲線近似曲線求方程根的疊代方法.設已知曲線y=f(二)_上三個點 重複上述步驟可算出二3,二...
資料分析插值法是公務員行政職業能力測驗中解答資料分析題目的一種快速比較分析數據的方法。...
埃特金逐步線性插值法(Aitken successive lin-ear interpolation method)一種能逐步升階的插值方法.用拉格朗日插值多項式計算函式近似值時,如果精度不滿足要求,需增加...
又稱插值法。根據未知函式f(x)在某區間內若干點的函式值,作出在該若干點的函式值與f(x)值相等的特定函式來近似原函式f(x),進而可用此特定函式算出該區間內...
