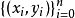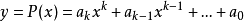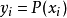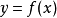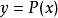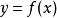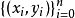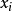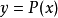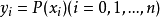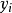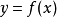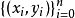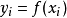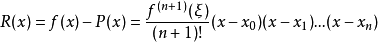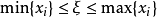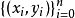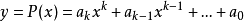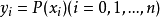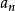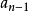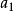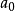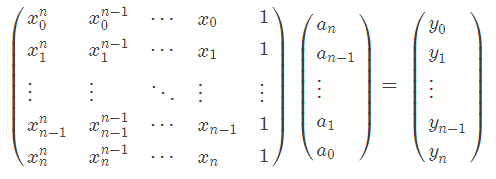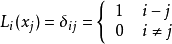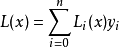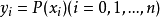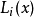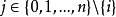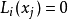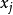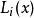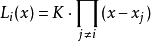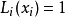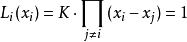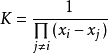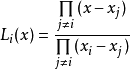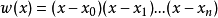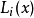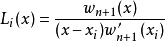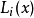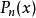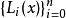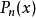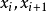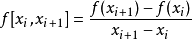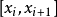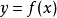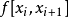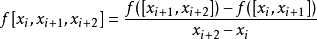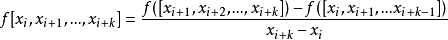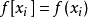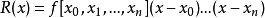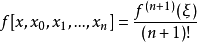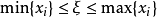定義
給定n+1個點
(稱為插值點),所謂多項式插值就是找到一個多項式(稱為插值
多項式)
其中,i=0,1,...,n。也就是說,多項式y=P(x)的圖像要經過給定的n+1個點。
在實際套用中,這些插值點可能來自某次實驗測量所得的數據,也可能來自某個複雜函式
的值。通過計算插值多項式,我們可以找到這些實驗數據間的規律,或者使用簡單的多項式函式
來近似複雜的函式
。
唯一性和誤差
定理一:
給定n+1個點
,若
兩兩不同,則存在
唯一一個次數不超過n的多項式
,使得
成立。
證明:利用范德蒙德矩陣和代數學基本定理即得。
當
的值來自某個函式
,且f(x)具有n+1階連續導數時,下面的定理可以用來計算多項式插值的(截斷)誤差。
定理二:
給定n+1個點
,其中
,進一步假設函式f(x)具有n+1階連續導數,則插值多項式P(x)的誤差R(x)為
計算方法
給定n+1個點, 計算插值多項式的主要方法有:直接法、拉格朗日多項式插值和牛頓多項式插值。下面我們分別介紹這三種方法。
(注意,根據定理一,這三種方法得到的插值多項式在理論上說應該是一致的,而且誤差也相同。)
直接法
根據定理一,假設插值多項式為
由插值條件
,我們得到關於係數
,
,…,
,
的線性方程組
通過求解這個線性方程組,即得到插值多項式。
優點:直接,性質一目了然。
缺點:待求解的線性方程組的係數矩陣為
范德蒙德(Vandermonde)矩陣,它是一個
病態矩陣,這使得在實際求解方程組時將產生很大的誤差。
拉格朗日多項式插值
拉格朗日(Lagrange)多項式插值的原理是:先構造一組
拉格朗日基函式 ,這些基函式為次數不超過n的多項式,且具有性質
然後將這些基函式做線性組合,得到拉格朗日插值多項式
由基函式的性質,當
時,
,即
為
的零點,可以假設
從而得到
定理三:令
為全體次數不超過n的多項式構成的集合,則
是線性空間
的一組基。
Matlab 實現
function [y,Lb] = LagrangeInterpolation(X,Y,x)% 拉格朗日多項式插值函式% 注意:插值點的個數為n,差值多項式的次數為n-1%% 輸入參數% X,Y: 插值點坐標% x: 求值點%% 輸出參數% y: 拉格朗日插值多項式在x點的值% Lb: 拉格朗日基函式在x點的值if length(X) ~= length(Y) error('X和Y的長度不相等'); endn = length(X); %獲取插值點的個數 %初始化 y = 0; Lb = ones(1,n); for i = 1:n for j = 1:n %計算拉格朗日基函式在x點的值 if j ~= i Lb(i) = Lb(i) * (x-X(j))/(X(i)-X(j)); end end y = y + Lb(i)*Y(i); %計算拉格朗日插值多項式的值 endend均差與牛頓多項式插值
牛頓多項式插值是基於均差的計算。首先定義均差如下:
用遞歸的方式,我們定義二階均差為
根據均差的定義,構造均差表如下:
如果將x也看作一個點,由均差的定義可以得到
稱為牛頓插值多項式。
由定理一和定理二得到均差和導數的關係如下:
Matlab實現
function [y,Nt]=NewtonInterpolation(X,Y,x)% 牛頓多項式插值函式% 注意:插值點的個數為n,差值多項式的次數為n-1%% 輸入參數% X,Y: 插值點坐標% x: 求值點%% 輸出參數% y:牛頓差值多項式在x點的值% Nt:均差表if length(X) ~= length(Y) error('X和Y的長度不相等'); endn = length(X); Nt = zeros(n); %初始化均差表,按列存放各階均差 Nt(1,1) = Y(1); %0階均差 for i = 2:n %按行計算均差表 Nt(i,1) = Y(i); %0階均差 for j = 2:i Nt(i,j) = (Nt(i,j-1)-Nt(i-1,j-1))/(X(i)-X(i-j+1)); end end %計算牛頓插值多項式在x點上的值w = 1; y = Nt(1,1) * w; for i = 2 : n w = w * (x - X(i-1)); y = y + Nt(i,i) * w; end end比較
拉格朗日多項式插值的計算量大於牛頓多項式插值的計算量。
特別地,當新增一個插值點時,拉格朗日插值需要重新計算全部的基函式,而牛頓插值只需計算均差表中新的一行的值即可。