不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應的導數值也相等,甚至要求高階導數也相等,滿足這種要求的插值多項式就是埃爾米特插值多項式。
基本介紹
- 中文名:埃爾米特插值
- 外文名:Hermite interpolation
- 學科:數理科學
- 別稱:Hermite插值
簡介
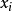
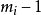
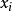
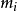
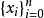
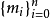
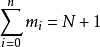
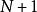

定義
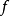
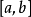
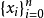
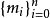
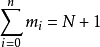
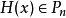
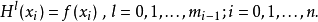

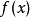
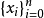
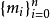
二重Hermite插值多項式
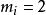
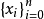
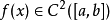
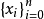

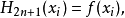
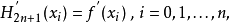
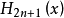
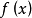
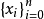
相關定理
1.唯一性定理
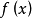
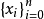
2.誤差定理
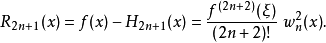
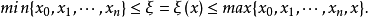
不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應的導數值也相等,甚至要求高階導數也相等,滿足這種要求的插值多項式就是埃爾米特插值多項式。
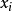
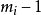
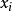
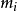
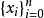
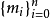
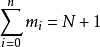
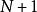

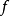
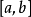
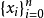
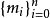
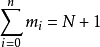
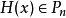
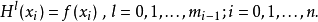

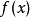
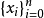
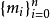
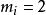
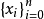
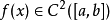
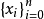

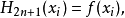
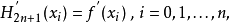
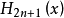
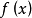
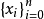
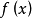
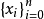
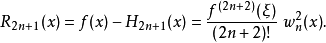
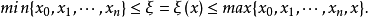
不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應的導數值也相等,甚至要求高階導數也相等,滿足這種要求的插值多項式就是埃爾米特插值多項式。...
埃爾米特插值公式(Hermite interpolation formina )區域上解析函式的拉格朗日插值多項式的積分表示式。不少實際的插值問題不但要求在節點上的函式值相等,而且還要求對應...
埃爾米特插值是一種常見的插值方法。埃爾米特插值多項式可以從各方面擴充。可以在某些結點處放棄對某些階導數的要求,這就是所謂伯克霍夫插值。...
這時的插值函式P(x),自然不僅要求在這些點等於f(x)的函式值,而且要求P(x)的導數在這些點也等於f(x)的導數值。這就是埃爾米特插值問題,也稱帶導數的插值問題...
帕爾型插值逼近(Pall-type interpolation approximation)是埃爾米特插值逼近的一個套用性拓廣。...
兩點三次帶導數插值是埃爾米特插值中最基本、最常用的一種(參見“埃爾米特插值”).詞條標籤: 科學 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 ...
伯克霍夫插值多項式逼近(approximation byBirkhoff interpolation polynomials)是埃爾米特插值多項式逼近的一種推廣。如果在埃爾米特插值過程中放棄在某些點處的某些階導數...
稱Hn(x)為n階埃爾米特多項式。它在[0,+∞)內有n個零點。常用作插值逼近中的結點。...... 為埃爾米特多項式系,而稱Hn(x)為n階埃爾米特多項式。它在[0,+∞...
插值法又稱“內插法”,是利用函式f (x)在某區間中已知的若干點的函式值,作出適當的特定函式,在區間的其他點上用這特定函式的值作為函式f (x)的近似值,這種...
埃爾米特-費耶爾插值多項式(Hermite-Fejer interpolation polynomials)是埃爾米特插值的一種特殊情況。...
6.4牛頓插值多項式6.4.1差商形式的牛頓插值多項式6.4.2差商的基本性質6.4.3差分形式的牛頓插值多項式6.5埃爾米特插值多項式6.5.1構造基函式方法...
1.2.1 線性插值1.2.2 二次插值1.2.3 n次拉格朗日插值多項式1.3 牛頓(Newton)型式1.3.1 差商及其計算1.3.2 牛頓插值1.4 *埃爾米特(Hermite)插值...
1.5.3 樣條插值 451.6 二元函式插值方法 501.6.1 雙線性插值 501.6.2 雙二次插值 521.6.3 雙三次插值 531.6.4 雙三次埃爾米特插值 54...
2.3.1 插值多項式的逐次生成(29)2.3.2 均差及其性質(30)2.3.3 牛頓插值多項式(31)2.3.4 差分形式的牛頓插值公式(32)2.4 埃爾米特插值(35)...
本書是為工科大學生學習“數值計算方法”課而編寫的教材,內容包括:插值與逼近,...2.3 牛頓(Newton)插值2.4 埃爾米特(Hermite)插值2.5 三次樣條插值...
5?2?3插值的逼近性質5?3埃特金逐步插值法5?4牛頓插值法5?4?1差商及其牛頓插值公式5?4?2差分與等距結點插值公式5?5埃爾米特插值法5?6樣條插值法...
1.5分段低次插值法與樣條插值法 1.5.1分段線性插值 1.5.2分段三次埃爾米特插值 1.5.3樣條插值 1.6二元函式插值方法 1.6.1雙線性插值 1.6.2雙二次插...
1.3差商與牛頓(Newton)插值 1.3.1差商的定義和性質 1.3.2Newton插值公式 1.4差分與等距節點插值 1.4.1差分及其性質 1.4.2等距節點插值公式 1.5埃爾米特(Her...
第2章 插值法 2.1 引言 2.2 幾次代數插值多項式 2.3 拉格朗日插值 2.4 牛頓插值 2.5 差分與等距節點插值 2.6 埃爾米特插值 2.7 分段低次插值 ...
4.2.2插值的誤差估計 4.2.3拉格朗日插值算法在計算機上的實現 4.2.4插值函式收斂性的進一步分析 4.3埃爾米特插值 4.3.1兩點三次埃爾米特插值 4.3.2n+1個節點埃爾...
第2章插值法2.1問題的提出2.2拉格朗日插值2.3牛頓插值2.4埃爾米特插值2.5分段低次插值2.6三次樣條插值第3章擬合與逼近3.1問題的提出...
2.4.2一般埃爾米特插值多項式2.4.3誤差估計2.5分段低次插值2.5.1高次多項式插值問題2.5.2分段低次插值2.6三次樣條插值2.6.1樣條插值函式的概念...
假如除了滿足函式值的插值條件外還滿足各類導數或高階導數的插值條件就得到埃爾米特插值多項式。對周期函式可仿照代數多項式構造拉格朗日三角插值多項式。...
第二章 多項式插值與樣條插值第一節 多項式插值第二節 拉格朗日(Langrange)插值第三節 牛頓(Newton)插值第四節 埃爾米特(Hermite)插值...
5.4.5牛頓差分插值的算法和程式1395.5埃爾米特插值1455.5.1埃爾米特插值簡介1455.5.22點3次埃爾米特插值1475.5.3帶1階導數的埃爾米特插值1485.5.4埃爾...
4.5 埃爾米特插值784.6 分段低次插值804.7 三次樣條插值824.8 曲線擬合的最小二乘法86小結89習題4 91第5章 函式逼近與計算945.1 最佳一致逼近多項式94...
第2章插值計算 2.1概述 2.2拉格朗日插值 2.3牛頓插值 2.4插值多項式的餘項 2.5埃爾米特插值 2.6樣條函式插值 2.7二元函式插值 習題 第3章回歸與...
第二章 函式插值第一節 多項式差值問題第二節 拉格朗日插值法第三節 牛頓插值法第四節 埃爾米特插值第五節 分段低次插值第六節 樣條插值習題二...
