伯克霍夫插值多項式逼近(approximation byBirkhoff interpolation polynomials)是埃爾米特插值多項式逼近的一種推廣。如果在埃爾米特插值過程中放棄在某些點處的某些階導數取值的要求,那么就稱這種插值多項式為伯克霍夫插值多項式。
基本介紹
- 中文名:伯克霍夫插值多項式逼近
- 外文名:approximation byBirkhoff interpolation polynomials
- 領域:數學
- 學科:數學分析
- 性質:埃爾米特插值多項式逼近的推廣
- 提出者:美國數學家伯克霍夫
概念,埃爾米特插值多項式逼近,多項插值法,人物簡介,
概念
伯克霍夫插值多項式逼近是埃爾米特插值多項式逼近的一種推廣。如果在埃爾米特插值過程中放棄在某些點處的某些階導數取值的要求,那么就稱這種插值多項式為伯克霍夫插值多項式。研究這種多項式對函式的逼近,稱為伯克霍夫插值多項式逼近。其中最簡單的是(0,2)插值,它是常見的缺項插值的一種。具體地說:設{xk}k=1是[a,b]上一組相異的點,要求一個次數≤2n-1的代數多項式Sn(f,x),使得:

埃爾米特插值多項式逼近
埃爾米特插值多項式逼近是拉格朗日插值多項式逼近的一種拓廣。設xn<xn-1<…<x1是[a,b]上的互異的點,給定一張數表:
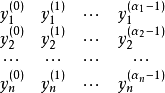

設f∈C[a,b],且f在xk處有αk-1階導數,若取y(s)k=f(s)(xk),則稱相應的埃爾米特插值多項式Hn(f,x)為f(x)的以{xk}k=1為結點組的(α1,α2,…,αn)階埃爾米特插值多項式。藉助於Hn(f,x)對f(x)在[a,b]上的逼近(包括一致逼近與平均逼近),都稱為埃爾米特插值多項式的逼近。若f∈C[a,b]在[a,b]上有m階導數,則:

多項插值法
多項式插值法是一種搜尋方法。指用插值多項式φ(t)的極小點逼近尋求函式f(t)的極小點的方法具體做法是:求φ′(t)=0的根,作為f(t)的極小點的近似,重複套用這一方法進行疊代計算,直到得出滿足事先給出的精度要求為止。用二次多項式逼近f(t),稱為二次插值法,用三次多項式逼近f(t),稱為三次插值法。
為了在n階多項式的向量空間Πn中構造唯一插值多項式。當使用Πn的單項式時,必須求解范德蒙德矩陣來構造插值多項式的係數ak。這可能是一個非常複雜的操作(按照計算機嘗試做這個工作的時鐘周期計算)。通過選擇Πn,可以簡化係數的計算,但是當用單項式表示內插多項式時,必須進行額外的計算。
1、一種方法是以牛頓形式的多項式插值法,並使用分差法來構建係數,例如,內維爾的算法。則將大量花費在O(n2)運算,而高斯消除則花費在O(n3)運算。此外,如果在數據集中添加額外的點,則只需要執行O(n)個額外的計算,而對於其他方法,則必須重做整個計算。
2、另一種是使用拉格朗日形式的多項式插值法。 所得公式立即顯示插值多項式存在於上述定理中所述的條件下。 當對計算多項式的係數不感興趣時,在計算p(x)的值(給定的x不在原始數據集中)時,拉格朗日公式將優於范德蒙德公式。 在這種情況下,我們可以將複雜度降低到O(n2)。
人物簡介
喬治· 戴維·伯克霍夫。數學家。生於密西根州歐弗里塞 (Overisel)。早年就讀於芝加哥劉易斯學院和芝加哥大 學。1905年畢業於哈佛大學。1907年在芝加哥大學獲 博士學位。先後執教於威斯康星大學(1907—1909)、普 林斯頓大學(1909—1912)。1911年升為數學教授。1912 年轉入哈佛大學(1912—1944),任數學教授(1919年起)、 珀金斯講座教授(1933年起)和哈佛大學藝術科學系主任 (1935—1939),兼任美國國家科學院院士以及丹麥科學 院、巴黎科學院院士,美國數學協會主席(1924—1926)、 美國科學促進會主席(1937年)、《數學年鑑》編輯。主要 研究數學分析和分析學在動力學中的運用。關於遍歷定 理的表述即所謂“強形式”對現代分析具有重要意義。提 出了自己的引力理論。對太陽系動力系統理論有傑出貢 獻。還把數學理論套用於美學和倫理學研究。主要論著 有《相對論與現代物理》、《動力系統》和《美學標準》等。 曾獲1918年奎里尼-斯坦帕利亞獎、美國數學協會的博 謝獎(1923年)。
