基本介紹
簡介,定義,伯恩斯坦不等式,共軛三角多項式,套用,
簡介
在數學中,三角多項式是一類基於三角函式的函式的總稱。三角多項式是可以表示成有限個正弦函式sin(nx) 和餘弦函式cos(nx) 的和的函式,其中的x 是變數,而n 是一個自然數。三角多項式中每一項的係數可以是實數或者複數。如果係數是複數的話,那么這個三角多項式是一個傅立葉級數。
三角多項式在許多數學分支,如數學分析和數值分析中都有套用,例如在傅立葉分析中,三角多項式被用於傅立葉級數的表示,在三角插值法中,三角多項式被用於逼近周期性函式。
定義
形如

的多項式,式中係數 ,
, 為任意給定的實數,
為任意給定的實數, 不全為零。
不全為零。 稱為此三角多項式的階數。任何一個三角多項式都是周期
稱為此三角多項式的階數。任何一個三角多項式都是周期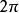 的周期函式,因此對於三角多項式的研究往往只要在長為
的周期函式,因此對於三角多項式的研究往往只要在長為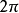 的半開區間中進行。任何兩個三角多項式的和、差、積仍然是個三角多項式,而且,若
的半開區間中進行。任何兩個三角多項式的和、差、積仍然是個三角多項式,而且,若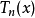 與
與 分別為
分別為 階與
階與 階三角多項式,且
階三角多項式,且 ,則
,則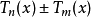 是個階不超過
是個階不超過 的三角多項式,
的三角多項式,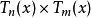 是階為
是階為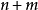 的三角多項式。利用歐拉公式
的三角多項式。利用歐拉公式




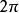
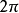
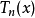




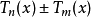

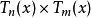
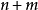

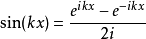
其中,



式中
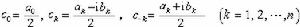 公式
公式

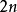



對於 階三角多項式
階三角多項式 ,記
,記


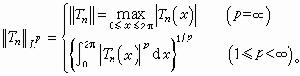 公式
公式常稱為Tn的Lp範數,若1≤p≤p┡≤∞,則

此外還有如下的尼科利斯基不等式

特別有

伯恩斯坦不等式
設Tn(x)是n階三角多項式,Tń(x)是它的導數,則有不等式
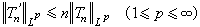
這是1912年С.Η.伯恩斯坦發現的,稱為伯恩斯坦不等式。其中係數n不能再減小,例如對任何常數A及α,Tn(x)=A sin(nx+α)都使它成等式。伯恩斯坦不等式在函式逼近論中起著重要的作用,並且有著各種拓廣。例如,С.Б.斯捷奇金於1948年證明,對任何n階三角多項式Tn(x)及自然數k,都有

共軛三角多項式
對給定的n階三角多項式Tn(x),記
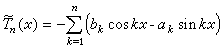
稱為Tn(x)的共軛三角多項式。對於共軛三角多項式的導數有不等式
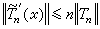
這裡係數n也是不能減小的。
應該指出,對於復係數三角多項式Tn(x)(即諸係數αk,bk為複數),同樣有

於是,對於自然數k,有
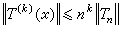
套用
自然,三角多項式是一類簡單的周期函式,但是,它是近似表示一般的周期函式的有效工具,隨著三角多項式的階的增高,任何連續的周期函式都可以藉助於三角多項逼近到預先給定的程度。反之如果已知這種逼近程度的收斂於零的速度,也就有可能推出被逼近函式的構造性質,這個事實本身是有著深刻的物理意義的,周期運動的分解便是一個明顯的例證。三角多項式是在其他數學、物理、力學等領域中有著廣泛的套用。