歐拉示性數

在代數拓撲中，歐拉示性數（Euler characteristic）是一個拓撲不變數（事實上，是同倫不變數），對於一大類拓撲空間有定義。

基本介紹

• 中文名：歐拉示性數
• 外文名：Euler characteristic
• 提出者：萊昂哈德·歐拉
• 適用範圍：數理科學

定義

如果一個拓撲空間 X 有有限的三角剖分 h：X→ |K|，X 的歐拉示性數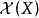定義為它的剖分復形 K 的各個維數單純形個數（即單純鏈復形的秩）的交錯和，即。

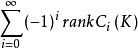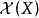
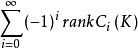
對於有限CW-復形(CW-Complex)包括有限單純復形(simplicial complex)，歐拉示性數可以定義為交錯和

其中表示維胞腔的個數。

然後，可以把流形的歐拉示性數定義為一個和它同胚的單純復形的歐拉示性數。例如，圓圈和環面其歐拉示性數為0而實心球歐拉示性數為1。

閉可定向曲面的歐拉示性數可以通過它們的虧格g來計算

閉不可定向曲面的歐拉示性數可以用下式通過它們的(不可定向)虧格k來計算

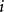
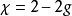
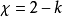
歐拉示性數和三角化的選擇無關。公式也可用於到任意多邊形的分解。

對於圓盤，我們有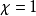, 對於平面我們有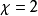, 數的時候把外面作為一個面。

對於閉流形，歐拉示性數和歐拉數,也就是其切叢的在流形的基本類上計算的歐拉類。

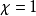
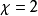
對於閉黎曼曲面，歐拉示性數也可以通過曲率的積分得到—參看對於二維情況的高斯-博內定理(Gauss-Bonnet)和對於一般情況的廣義高斯-博內定理。高斯-博內定理的離散情況的對應是笛卡兒定理，它表明多面體用完整圓圈測量的“總虧量” ，是多面體的歐拉示性數；參看虧量。

更一般的，對於所有拓撲空間，我們可以定義第n個貝蒂數作為第n個同調群的階。歐拉示性數可以定義為如下交換和

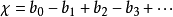
這個定義在貝蒂數全都有限並且在一個特定指標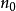以外為0時有意義。

兩個同倫的拓撲空間有同構的同調群，所以有相同的歐拉示性數。

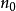
從這個定義和龐加萊對偶性，可以得到所有閉合奇數維流形的歐拉數為0的結論。

如果M和N是拓撲空間，則它們的積空間M×N的歐拉示性數為

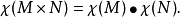
經典公式

有關歐拉示性數的一個經典的公式是

其中 是拓撲空間 X 的第 i 個貝蒂數，這一公式稱為歐拉-龐加萊公式。該公式亦說明了歐拉示性數不依賴於剖分的選取，是一個拓撲不變數。

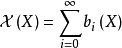
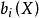
由此，歐拉示性數可作進一步推廣。對於任意一個拓撲空間 X，當求和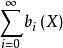 存在時，這一整數稱為拓撲空間 X 歐拉示性數。

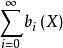
歷史

第一個歐拉公式的嚴格證明，由20歲的柯西給出，大致如下:

圖1

從多面體去掉一面，通過把去掉的面的邊互相拉遠，把所有剩下的面變成點和曲線的平面網路。不失一般性，可以假設變形的邊繼續保持為直線段。正常的面不再是正常的多邊形即使開始的時候它們是正常的。但是，點，邊和面的個數保持不變，和給定多面體的一樣(移去的面對應網路的外部。

重複一系列可以簡化網路卻不改變其歐拉數（也是歐拉示性數）F−E+V的額外變換。

1、若有一個多邊形面有3條邊以上，我們劃一個對角線。這增加一條邊和一個面。繼續增加邊直到所有面都是三角形。
2、除掉只有一條邊和外部相鄰的三角形。這把邊和面的個數各減一而保持頂點數不變。
3、（逐個）除去所有和網路外部共享兩條邊的三角形。這會減少一個頂點、兩條邊和一個面。

重複使用第 2 步和第 3 步直到只剩一個三角形。對於一個三角形F=2（把外部數在內），E=3 ，V=3 。所以F−E+V=2 。證畢。

偏序集

有界偏序集(partially ordered set,簡稱poset)的歐拉示性數的概念是另一種推廣，在組合論中很重要。一個偏序集“有界”，如果它有最小和最大元素，我們把它們叫作 0 和 1 。這樣一個偏序集的歐拉示性數是 μ(0,1) ，其中 μ 是在偏序集的相交代數(incidence algebra)中的默比烏斯函式。