簡介 數學上,特別是在複分析中,一個黎曼曲面是一個一維
複流形 。黎曼曲面可以被認為是一個
複平面 的變形版本:在每一點局部看來,他們就像一片複平面,但整體的拓撲可能極為不同。例如,他們可以看起來像球或是環,或者兩個頁面粘在一起。
黎曼曲面的要點在於在他們之間可以定義
全純函式 (holomorphic function)。黎曼曲面被認為是研究這些函式的整體行為的自然選擇,特別是像
平方根 和
自然對數 這樣的
多值函式 。
函式 f(z) = sqrt(z) 的黎曼曲面 每個黎曼曲面都是二維實解析流形(也就是曲面),但它有更多的結構(特別是一個復結構),因為多值函式的無歧義的定義需要用到這些結構。一個實二維流形可以變成為一個黎曼曲面(通常有幾種不同的方式)若且唯若它是可定向的。所以球和環有復結構,但是
莫比烏斯圈 ,
克萊因瓶 和投影平面沒有。
詳細說明 單值 解析函式的
反函式 可以是多值的。例如,
冪函式 和
指數函式 的反函式為
根式 函式和
對數函式 ,它們都是多值的。另外,從一個解析函式元素出發沿一個閉曲線作
解析開拓 ,最後可能得到不同的元素。因此,完全解析函式往往是多值的。在研究 多值函式時,人們先把它分解為一個個單值解析 分支,然後按這些分支之間的關係把它們連線起來。 為研究,把擴充的複平面沿正
實軸 割開,記為╦1,它的邊界是兩條正實軸Л劑和Л奐,分別鑲在
第一象限 的下邊和
第四象限 的上邊,在╦1上 令
黎曼曲面 就得到的一個
單值 解析分支,它在╦1的內部是解析的,並且連續到邊界Л劑和Л奐上, 但在和同一個
正實數 x 對應的分別位於Л劑 和Л奐上的兩個點上,卻分別取不同的值。設╦ 2是另一個沿正
實軸 割開的擴充的複平面,它的邊界記為Л崹 和Л崍 。令就得到的另一個單值解析分支。與不同,在Л崹和Л崍 上與
正實數 x 對應的兩個點處,的值分別是。由於在 Л劑和Л奐上的值分別與在Л崍和Л崹上的值相同,人們自然地把Л劑 和Л崍以及Л奐和Л崹兩兩粘接起來,而把╦1和╦2拼接成一個整體,這就是的黎曼曲面。作為定義在這個曲面上的函式,包含了它的兩個分支,同時是
單值 的。替
多值函式 構造一個適當的定義場所,而使得它成為一個完整的單值解析函式,這是黎曼的原始的思想。這樣構造出來的,和ln
z 的黎曼曲面如圖1所示。
黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 黎曼曲面 把的黎曼曲面按原來的位置放在擴充的複平面上就成了擴充複平面的一個
n 葉覆蓋曲面。曲面上的點
O 和∞叫做
n -1級枝點。同樣,ln
z 的黎曼曲面是(除去原點後的)複平面的無枝點的覆蓋曲面。一般地說,複平面(或擴充的複平面)的任意的一個覆蓋曲面都可看作一個黎曼曲面。設覆蓋曲面中的點
P 位於複平面中的點
z 之上,則稱
z 為
P 的投影。定義在曲面上的一個函式在非枝點處是否解析,就看它作為投影
z 的函式是否是解析的;而在投影為
z 0的
n -1級枝點處,則要看它對於是否是解析的。這就是黎曼本人的原始的黎曼曲面的概念。黎曼曲面的經典理論是在這樣的概念上發展起來的。
黎曼曲面 一個完全解析函式或完全解析構形,把其中以
z 0為中心的函式元素看作放在
z 0上的點,自然就成了擴充平面的覆蓋曲面,這就是它的黎曼曲面。一個
代數 函式
w =
w (
z )的黎曼曲面是擴充平面的
n 葉覆蓋曲面(
n 為對應的方程中
w 的最高次數)。例如,的黎曼曲面的構造如圖2所示。把上下兩個平面中連線0,1和連線2,3的兩個線段都割成裂縫,每一裂縫產生兩條邊,分別與平面上半部分和下半部分相連,用實線與虛線表示。然後把上平面中實線(虛線)所示的邊和下平面中虛線(實線)所示的邊粘接起來。
黎曼曲面 (C.H.)H.外爾首先給出黎曼曲面的近代定義。與此同時,他也給出了"流形"這個近代數學的基本概念的嚴格定義。按照外爾的觀點,黎曼曲面就是一維的複流形。在一個曲面(局部與歐氏平面同胚的、連通的豪斯多夫空間) 上,定義了一族局部參數(曲面的某一個
開集 上的一個連續單葉復值函式,也叫局部坐標),若在任意兩個相鄰的局部參數的
定義域 的公共部分上,其中的一個參數作為另一個參數的函式是解析的,並且這些參數的定義域覆蓋了整個曲面,那么,這個曲面連同這族局部參數(叫做共形結構)就構成了一個黎曼曲面。複平面
C 或者
C 上任一個區域按其自然參數都是黎曼曲面。在擴充複平面╦上,除了在
C 上已有一個自然參數外,再在區域{
z ││
z │>0}(包括
無窮遠點 )上令,得另一參數,而使╦成為一個黎曼曲面。一個黎曼曲面到黎曼曲面里的連續映射稱為是解析的,如果它用兩個曲面上的局部參數表示出來是
解析函式 。一個黎曼曲面到 ╦里的解析映射就是該曲面上的
半純函式 (
亞純函式 )。黎曼曲面上的調和(或次調和)函式的定義為關於局部參數是調和(或次調和)的函式。黎曼曲面的引入大大地開擴了
複變函數論 的研究範圍。
由緊曲面作成的黎曼曲面叫做閉黎曼曲面,否則就叫做開黎曼曲面。若一個
閉曲面 (或開曲面)上的一維同調群(或模理想邊界的一維同調群)的秩是2
g ,則稱
g (非負整數或無窮)為此黎曼曲面的
虧格 。開曲面的虧格可能為無窮。兩個黎曼曲面稱為是共形等價的,如果存在一個從一個曲面到另一個曲面上的一一的解析映射(
共形映射 )。同一個虧格
g (
g >1)的閉黎曼曲面的所有共形
等價類 組成所謂
模空間 。黎曼首先發現,模空間中的元素由3
g -3個復參數確定。從模空間的研究中產生出豐富多彩的
泰希米勒空間 的理論。
人們還把開黎曼曲面作了分類。不存在非常數的負次調和函式的開曲面叫做拋物型曲面,其他的開曲面就叫做雙曲型曲面。拋物型曲面所成的類用
O G表示。不存在非常數的有界解析或調和函式,狄利克雷積分為有窮的解析或調和函式,或正調和函式的開曲面分別組成類
O AB或
O HB,
O AD或
O HD,或
O HP。在這些曲面類之間存在如下的包含關係:按照黎曼本人的原始概念,黎曼曲面是╦ 的覆蓋曲面。所謂曲面愞 是曲面
F 的覆蓋曲面,是指存在曲面
愞 到曲面
F 里的映射
ƒ ,對於每一個
慉 ∈愞,都存在慉和
ƒ (慉)∈
F 的開鄰 和
V ,使得限制和
V 之間,
ƒ 拓撲等價於單位圓到自身的映射
z =
z n(n是正整數,它與慉有關;當n>1時,慉叫做枝點)。定義中的映射ƒ叫做投影。當F是一個黎曼曲面時,可使上面的是F 的局部參數。令z為愞的局部參數,就在愞上定義了一個共形結構,而使它成為一個黎曼曲面,並且,ƒ是一個解析映射。一個完全解析函式w =g(z)的黎曼曲面就是╦的覆蓋曲面,並按上面的方法賦以共形結構。在這個曲面上有兩個半純函式:把w=g(z)看作曲面上的單值函式,記以w=G(P);還有從曲面到╦上的投影,記以z=Z(P),P是曲面上的點。這裡的完全解析函式可以包含極元素和分枝元素,以及分枝的極元素。 在一個曲面上有相同的起點和相同的終點的兩條曲線(連續曲線)уi:t→φi(t)(0≤t≤1,i=1,2) 稱為是同倫的,如果存在到這個曲面里的連續映射(t,u)→φ(t,u)(0≤t≤1,0≤u≤1),使得φ(t,0)呏φ1(t),φ(t,1)呏φ2(t),φ(0,u)呏φ1(0),φ(1,u)呏φ1(1)。曲面上固定端點的閉曲線組成的所有同倫等價類以曲線的連線作為乘法運算組成一個群,叫做曲面關於這個定點的基本群。關於不同點的基本群是互相同構的。基本群只包含一個元素的曲面叫做單連通曲面。 沒有枝點的覆蓋曲面叫做光滑覆蓋曲面。設ƒ使愞成為F 的光滑覆蓋曲面。若у=ƒ(),其中的和у分別是愞和F上的曲線,則稱是у的提升。若對於任意的у嶅F和任意的以у的起點為投影的慉∈愞,у的以慉為起點的提升總是存在的,則稱愞是F的正規覆蓋曲面。光滑性保證指定起點的提升的惟一性。單值性定理稱:若愞是F的正規覆蓋曲面,則對於F上的任意兩條互相同倫的曲線v1和v2以及愞中任意的以v1和v2的公共起點為投影的點慉,v1和у2的以慉為起點的提升和2總有公共的終點,並且,1和2也是同倫的(在 愞上)。複變函數論中關於解析函式元素沿曲線解析開拓的單值性定理是這個定理的一個具體套用。 單連通的正規覆蓋曲面叫做萬有覆蓋曲面。對於任意的一個曲面F,它的萬有覆蓋曲面愞總是存在而且在共形等價的意義下是惟一的。當F是一個黎曼曲面時,可使愞也成為一個黎曼曲面,而投影ƒ是解析映射。著名的單值化定理稱:單連通的黎曼曲面一定共形等價於 ╦(閉)、C(拋物型)或單位圓(雙曲型)。若愞=╦,則F=╦。如果愞 =C,則F =C,C \{0}, 或是環面(環面就是虧格為1的閉曲面;反過來, 環面的萬有覆蓋(黎曼)曲面一定是C)。當愞是單位圓時,所有滿足ƒ。φ=ƒ 的共形映射φ(叫做覆蓋變換)組成一個富克斯群。因此,除去上面幾種特例外,每一個黎曼曲面都可表示成單位圓關於一個富克斯群的商;因而,分式線性變換組成的間斷群(即克萊因群,包括富克斯群)的理論和黎曼曲面理論有緊密的聯繫。若這裡的F是完全解析函式w=g(z)的黎曼曲面,則G(ƒ(t))和Z(ƒ(t))(t∈╦,C,或單位圓)都是半純函式,多值函式w=g(z)經參數t(叫做單值化參數)單值化了。從而就解決了著名的希爾伯特第22問題即單值化問題。 在一個黎曼曲面上,若對每一個局部參數z都定義了一個微分ƒ(z)dz(ƒ(z)是半純函式), 而與相鄰的兩個參數z和ζ 對應的ƒ(z)dz和φ(ζ)dζ 滿足關係ƒ(z(ζ))·z┡(ζ)=φ(ζ),則稱在曲面上定義了一個半純微分。半純函式(或半純微分)在某一點的零點或極點的級等於在取定一個局部參數後該函式(或該微分在這個參數下的表示形式中的係數)作為這個局部參數的函式在該點的零點和極點的級。黎曼-羅赫定理稱:在一個虧格為g的閉曲面上,指定了點p1,p2,…,ps;q1,q2,…,qt和正整數k1,k2,…,ks;n1,n2,…,nt,令。設以pi為至多ki級極點(或至少ki級零點,i=1,2,…,s),並且以qi為至少ni級零點(或至多ni級極點,i=1,2,…,t)的所有半純函式(或半純微分)組成的複數域上的線性空間的維數為A(或B),那么,A=B +m-g+1。這個定理是閉黎曼曲面理論的一個基本結果;在一定條件下,也被推廣到開曲面和高維複流形。
黎曼曲面 舉例說明 黎曼曲面的幾何性質是最妙的,它們也給向其它曲線,
流形 或
代數簇 上的推廣提供了直觀的理解和動力。Riemann-Roch 定理就是這種影響的最佳例子。
令X為一個
豪斯多夫空間 (Hausdorff space)。一個從開子集U⊂X到C的子集的
同胚 稱為圖(chart). 兩個有重疊區域的圖f和g稱為兼容,如果映射f o g-1 和g o f-1 是在
定義域 上全純的。若A一組相容的圖,並且每個X中的x都在某個f的定義域中,則稱A為一個圖集(atlas)。當我們賦予X一個圖集A,我們稱(X,A)為一個黎曼曲面。如果知道有圖集,我們簡稱X為黎曼曲面。
不同的圖集可以在X上給出本質上相同的黎曼曲面結構;為避免這種模糊性,我們有時候要求X為極大的,也就是它不是任何一個更大的圖集的
子集 。根據佐恩引理(Zorn's Lemma)每個圖集A包含於一個唯一的最大圖集中。
複平面C可能是最平凡的黎曼曲面了。映射f(z) = z (
恆等映射 )定義了C的一個圖,而 是C的一個圖集. 映射g(z) = z* (
共軛 )映射也定義了C的一個圖而也是C的一個圖集. 圖f和g不相容,所以他們各自給了C一個黎曼曲面結構。事實上,給定黎曼曲面X及其圖集A, 共軛圖集B = {f* : f ∈ A} 總是不和A相容, 因此賦予X一個不同的黎曼曲面結構。
類似的,每個複平面的開
子集 可以自然的視為黎曼曲面。更一般的,每個黎曼曲面的開子集是一個黎曼曲面。
令S = C ∪ {∞} 並令f(z) = z 其中z 屬於S \ {∞} 並且令g(z) = 1 / z 其中z屬於S \ 以及 定義1/∞為0. 則f 和g為圖,它們相容,而{ f, g }是S圖集, 使S成為黎曼曲面。這個特殊的曲面稱為
黎曼球 因為它可以解釋為把複平面裹在一個球上。不象複平面,它是一個緊空間。
埃舍爾的《畫廊》也運用了黎曼曲面。
緊黎曼曲面可以視為和定義在
複數 上的非奇異
代數曲線 等效。非緊黎曼曲面的重要例子由解析連續給出
兩個黎曼曲面M和N之間的 函式f : M → N稱為全純(holomorphic),如果對於M的圖集中的每個圖g和N的圖集中的每個圖h,映射h o f o g-1 在所有有定義的地方是全純的(作為從C到C的函式) 。兩個全純函式的複合是全純的。兩個黎曼曲面M和N稱為保角等價(或共形等價conformally equivalent),如果存在一個
雙射 的從M到N的全純函式並且其逆也是全純的(最後一個條件是自動滿足的所以可以略去)。兩個保角等價的黎曼曲面對於所有的實際套用來講是完全相同的。
每個
單連通 的黎曼曲面和C或
黎曼球 C ∪ {∞}或開圓盤{z ∈ C : |z| < 1}保角等價。這個命題稱為一致化定理。
每個
連通 黎曼曲面可以轉成有常數
曲率 -1,0或1 的
完備 實
黎曼流形 。這個黎曼結構除了
度量 的縮放外是唯一。有曲率-1的黎曼曲面稱為雙曲的;開圓盤是個經典的例子。有曲率0的黎曼曲面稱為拋物的;C是典型的拋物黎曼曲面。最後,有曲率+1的黎曼曲面稱為橢圓的;
黎曼球 C ∪ {∞}是這樣的一個例子.
對於每個閉拋物黎曼曲面,
基本群 同構於2階格群,因而曲面可以構造為C/Γ,其中C是複平面而Γ 是格群。
陪集 的代表的集合叫做基本域。
類似的,對每個雙曲黎曼曲面,基本
群同構 於Fuchsian 群,因而曲面可以由Fuchsian 模型H/Γ 構造,其中H是上
半平面 而Γ是Fuchsian 群。H/Γ陪集的代表是自由正則集,可以作為度量基本多邊形。
當一個雙曲曲面是緊的,則曲面的總面積是4\pi(g-1), 其中 g 是曲面的虧格(genus);面積可由把Gauss-Bonnet 定理套用到基本多邊形的面積上來算出。
前面我們提到黎曼曲面,象所有複流形,象實流形一樣可定向。因為復圖f和g有變換函式h = f(g-1(z)),我們 可以認為h是從R2開集到R2的映射,在點z的雅戈比陣也就是由乘以複數h'(z)的運算給出的實線性變換。但是,乘以複數α的
行列式 等於|α|^2, 所以h的雅戈比陣有正的行列式值。所以,復圖集是可定向圖集。
相關介紹 黎曼 (G.F.B Riemann)1826年9月17日生於德國漢若威的布雷斯塞論茨,1866年7月20日卒於義大利塞拉斯卡。
黎曼是對
現代數學 影響最大的數學家之一,我們從他當時的數學水平來看,他作為偉大的分析學家,其成就可以分為八個領域來論述。前4個領域是關於
複分析 方面的,他第一個有意識的將實域過渡到復域,開創了複變函數域,
代數 函式論,常微分方程解析理論及
解析數論 諸方向;後4個領域主要涉及實分析,在積分理論,三角級理論,
微分幾何學 ,數學物理方程等方面取得重大突破。重要的是一個多世紀之前的成就卻直接同現代數學中的
拓撲 方法,一般流形概念,聯繫拓撲與分析的黎曼-洛赫定理,
代數幾何學 特別是阿貝爾簇以及參模等緊密相連,他的
空間觀念 及
黎曼幾何 更預示著
廣義相對論 ,正是他促發了現代數學的革命性變革。
黎曼是牧師之子,在哥廷根 (Gottingen) 大學和梅林大學學習,1851年在哥廷根大學獲得博士學位,1854年任該大學兼職講師,1857年任副教授,1859年作為P. G. L. Dirichlet的繼承人任教授。因患肺病,英年早逝。短短一生中,在數學各個領域作出了劃時代的貢獻。最重要的貢獻有四個方面:幾何學、複變函數論、微分方程和數學分析的基本理論。他是黎曼幾何的創始人,複變函數理論創始人之一。在數學分析方面,他給積分下的標準定義,一直沿用至今,以至於這種意義下的古典積分叫作“黎曼積分”。他還對傅立葉級數理論做了許多研究,其中最著名的就是以他的名字命名的定理。黎曼對偏微分方程和常微分方程理論,特別是常微分方程的奇點理論,也都創造了一些重要的方法。黎曼還十分關注自然科學,特別是物理學。他的複變函數和微分方程研究都直接與流體力學和電磁理論相聯繫,著名的數學家克萊因曾在《19世紀數學發展講義》一書中指出: “黎曼用他的數學才能為自然科學本身開闢新的途徑。然後又把自然科學作為形成數學中的新概念的動力”。
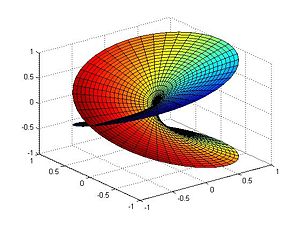 函式 f(z) = sqrt(z) 的黎曼曲面
函式 f(z) = sqrt(z) 的黎曼曲面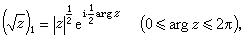 黎曼曲面
黎曼曲面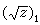 黎曼曲面
黎曼曲面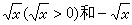 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面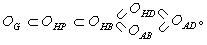 黎曼曲面
黎曼曲面
 函式 f(z) = sqrt(z) 的黎曼曲面
函式 f(z) = sqrt(z) 的黎曼曲面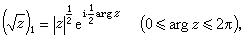 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面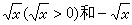 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面 黎曼曲面
黎曼曲面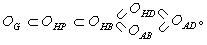 黎曼曲面
黎曼曲面