基本介紹
- 中文名:共形映射
- 外文名:conformal mapping
- 所屬學科:數理科學
- 別名:保角變換
概述


 圖1.直角格線和它在共形映射f下的像
圖1.直角格線和它在共形映射f下的像定義

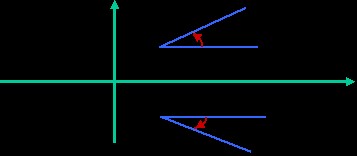 圖2.第二類保角映射圖例
圖2.第二類保角映射圖例定理









 圖1.直角格線和它在共形映射f下的像
圖1.直角格線和它在共形映射f下的像
 圖2.第二類保角映射圖例
圖2.第二類保角映射圖例





共形映射是複變函數論的一個分支,它從幾何的觀點來研究複變函數,其通過一個解析函式把一個區域映射到另一個區域進行研究。這個性質可以將一些不規則或者不好用...
多邊形映射是一類特殊的共形映射,一類把上半平面雙方單值共形映射成多角形區域的映射。它是由克里斯托費爾-施瓦茲公式確定的映射。...
共形反常是一種在量子化過程中出現的一個現象。共形反常在重整化後才物理意義,而引起物質能動張量反常的原因則為背景時空的非平直性。...
數學上,共形對稱即共形變換(英語:Conformal map),或稱保角變換,來自於流體力學和幾何學的概念,是一個保持角度不變的映射。...
設D(D⊂C)是單連通區域,且其內部含有原點O。若共形映射ω=φ(z)將D映成{ω||ω|<R0},並使φ(0),|φ'(0)|=1,則稱R0=R0(D)為D關於0的內映射...
黎曼-羅赫定理給出閉黎曼曲面上亞純函式構成的線性空間的維數,兩黎曼曲面,如果存在映一個為另一個的共形映射,則稱它們是共形等價的。...
數學上,度量空間之間的擬對稱映射,是雙利普希茨映射的一個推廣。雙利普希茨映射...擬對稱映射和擬共形映射也有關係,因為在很多情況這兩者其實等價。 [1] ...
克里斯托菲爾-施瓦茲公式是多角形區域共形映射函式的表達式。...... 共形映射到多角形區域G的單葉解析函式,z平面實軸上的n個點a1,a2,...,an(-∞<a1<a2<......
茹科夫斯基變換是在機翼理論中最基本的一種共形映射。這個函式在理論上及共形映射的實際構造上都是重要的。...
黎曼定理指出某些區域可用單葉函式共形映射成圓盤,但無法說明已給區域與圓盤的邊界之間是否有對應關係。對於以約當曲線為邊界的區域,有一個比較簡單的結果。...
褚玉明,湖州師範學院學科規劃與建設處處長。自1988年以來,長期從事擬共形映射、Kleinian群、函式不等式理論與套用的研究工作,近年來對控制理論產生興趣並已取得了一...
全書包括基本概念、共形映射、函式論的邊值問題及其套用、共形映射的變分原理、函式論在分析上的套用、運算元法及其套用、特殊函式等。...
在複變函數的套用上,共形映射具有重要的地位。H.E.茹科夫斯基通過共形映射研究繞機翼的流動便是著名的例子。實際套用中,常常要藉助近似方法具體地構造出映射函式...
內容簡介 克里斯托費爾一施瓦茲公式(Christoffel-Schwa- rz formula)多角形區域共形映射函式的表示式. 設w=f(z)是將上半平面D;Imz}O共形映射到多角形區域G的單葉...
令z為愞的局部參數,就在愞上定義了一個共形結構,而使它成為一個黎曼曲面,並且,ƒ是一個解析映射。一個完全解析函式w =g(z)的黎曼曲面就是╦的覆蓋曲面,...
分式線性變換是最簡單的共形映射,同時也是共形映射一般理論的基礎,並且具有許多幾何直觀十分明顯的重要性質。在建立邊界為圓弧或直線的區域之間的共形映射時,分式線性...
我們將繼續這方面的探索,並已在將有關結論向擬共形映射和多複變函數拓廣方面做了一些工作。⒉亞純函式的值分布論自上世紀二十年代創立以來,一直是複分析研究中...
單值化定理(uniformization theorem)是黎曼曲面理論中最基本最重要的定理。單值化定理表明,大多數的情形下,黎曼曲面共形等價於單位圓D對某個富克斯群G的商空間D/G...
