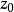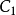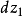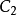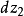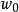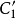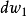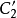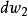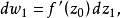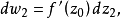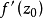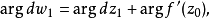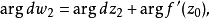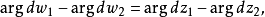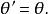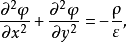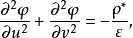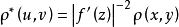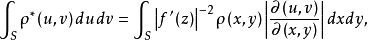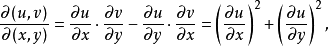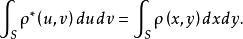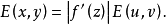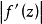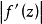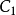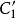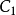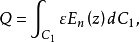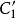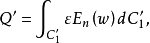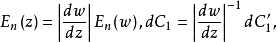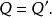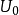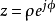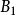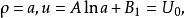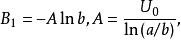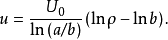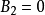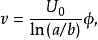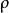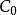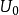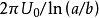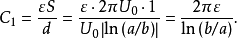基本知識
當
變換為
單值函式時,對於Z平面上的一個點
,在W平面就有一點叫
與之對應;對於Z平面上的一條曲線C,W平面就有一條曲線C'與之對應;同樣,在Z平面上的一個圖形D,也在W平面就有一個圖形D'與之對應,這種對應關係稱為
映射,或稱為
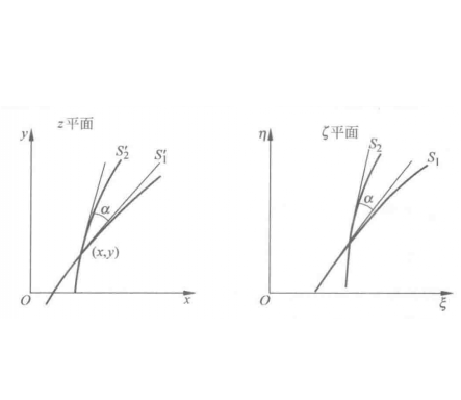
變換.如圖1所示。在這種變換中,儘管圖形的形狀要發生變化,但是相應的兩條曲線之間的夾角卻保持不變,所以該變換也叫做
保角變換。
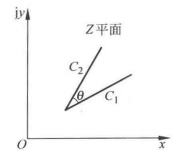 圖1(a)
圖1(a)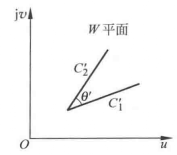 圖2(b)
圖2(b)為了證明保角性,設Z平面的
點,沿曲線
有一個增量
,沿曲線
有一個增量
;相應的W平面的
點,沿曲線
有一個增量
,沿曲線
有一個增量
,於是
這樣就證明了
保角性。在變換前後,圖形的形狀要產生旋轉和伸縮,但是兩條曲線之間的夾角保持不變。使用保角變換法求解靜態場問題的關鍵是選擇適當的變換函式,將Z平面上比較複雜的邊界變換成W平面上較易求解的邊界。
注意事項
使用保角變換應注意以下幾點。
式中,
。這表明,二維平面場的電荷密度經過變換以後要發生變化,但是電荷總量不變,其理由是
(2) 在變換前後,Z平面和W平面對應的電場強度要發生變化,它們之間的關係為
這是因為,從Z平面變換到W平面時,線元的長度要伸長
倍,相應的電場強度要減小
倍。
(3) 變換前後,兩導體之間的電容量不變。這裡的電容是指單位長度的電容。因為變換前後兩個導體之間的電位差不變,兩導體面上的電場和電荷密度發生了變化,但是,導體上的電荷總量不變。如取
為Z平面上導體表面,
為變換以後W平面上的導體表面,則沿軸線方向單位長度的
上的總電荷為
可以使用這個性質方便地計算兩個導體之間的電容量。
例題解析
例1 設無限長同軸線的內導體半徑為
,電位為
;外導體內半徑為b,電位為零。內、外導體間充滿介電常數為
的均勻介質。試計算同軸線的電位分布及單位長度的分布電容。
解:套用對數形式的複變函數計算電位分布。因為是二維平面場,在Z平面上導體邊界形狀是圓,所以選擇u為等位線。
因此,Z平面上u是以軸心為圓心、以
為半徑的一簇同心圓。
Z平面上內、外導體間的介質區域,通過保角變換變為W平面上一長方形區域。在W平面上計算單位長度電容
,只需求出距離為
、寬度為
的平板電容器的單位長度電容,所以計算要簡單得多。

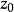
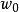
 圖1(a)
圖1(a) 圖2(b)
圖2(b)