復勢(complex potential)與複變函數論在流體力學中的套用有關的一個概念。設有一不可壓縮流體做平面定常運動，其速度向量v=(u,v)，其中無源、無匯，也無渦流。這些說明它等價於v=u+iv，為解析函式，稱為流體的復速度，其與積分路徑無關，稱為流體的復勢。
基本介紹
- 中文名：復勢
- 外文名：complex potential
- 套用領域：力學術語
- 範疇：理工科
- 定義：在流體力學中的套用有關的一概念
- 因素：數學原理
概念,基本原理,複函數,復速度,保角變換,套用領域,
概念
在勢流中，問題一般涉及在適當的邊界條件下解拉普拉斯方程
和
。合適的邊界條件通常是：在無窮遠處流動均勻或為零，和流體不能穿過它所繞流的固體表面。然而，除了對於某些簡單形狀
和
可以解調和方程或直接積分
容易地求得外，在速度已知時，最好用復變數理論和保角變換來確定 和 。
基本原理
複函數
在二維問題中，定義一個函式
（稱為復勢）的充要條件是 和 為調和函式及滿足柯西-黎曼方程。複函數定義為：
一般
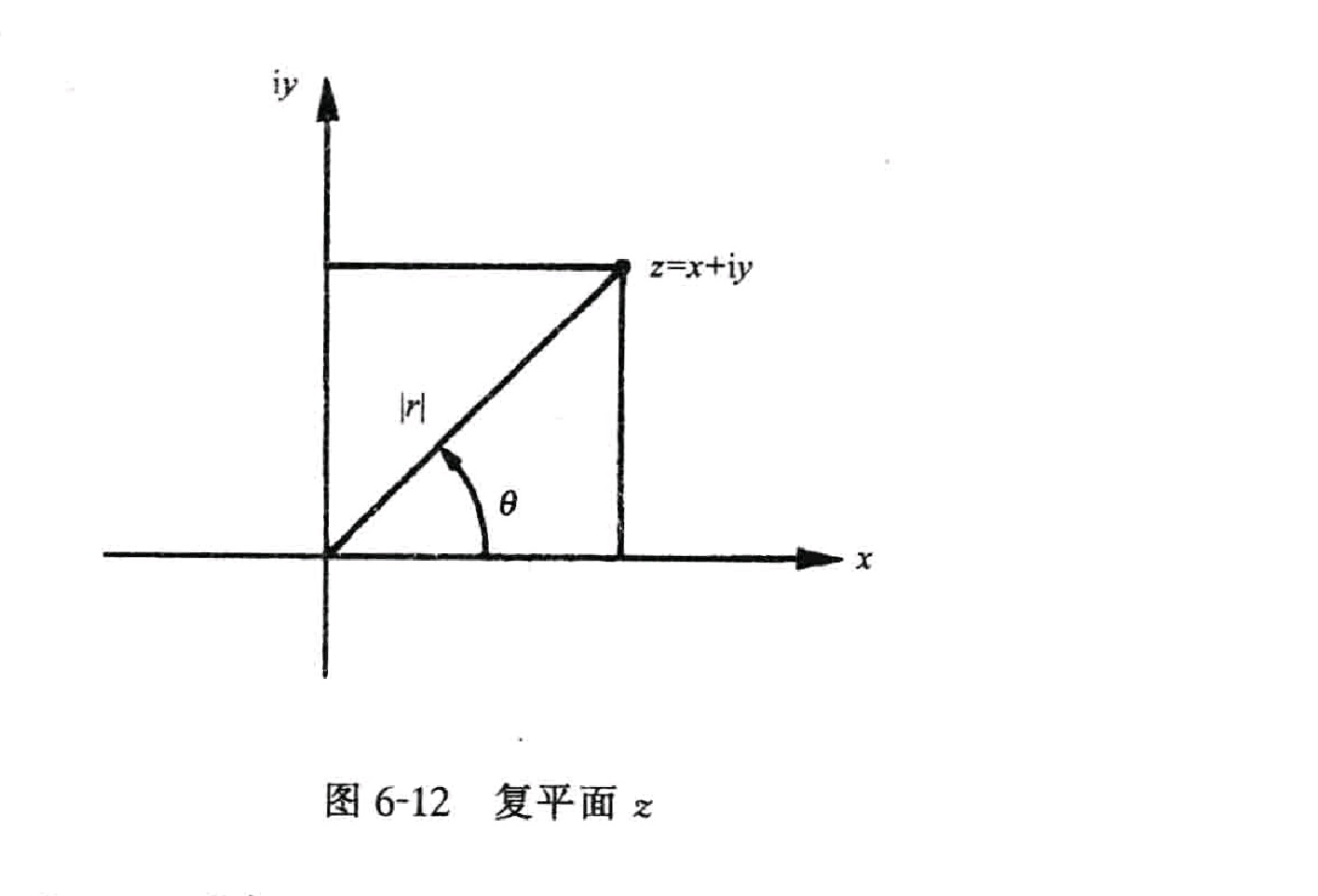圖1-1見圖1-1， 為具有實數部分 和虛數部分 的複數， 可以寫作為 的函式，因此， 的實數部分為
及虛數部分為
。
柯西-黎曼條件連同 和 單值及 和 的所有偏導數連續等條件意味著 是可析（或正則）函式。可析函式
是這樣的函式，（1）在一封閉廓線
內為有限值並為單值，及（2）所有導數存在並為單值。一個 的可析函式的實數部分和虛數部分稱為共軛函式並且是調和的。 和 是共軛函式並且我們知道
。
參照圖1-1，
可以對任意
進行計算。如果我們取 平行於 軸，我們有
及
如果取 平行於 軸，我們有
並且
復速度
對複函數 微分，我們得到
保角變換
發生運動的物理平面是或
平面，在該平面，
為常數的線為曲線並且代表流線。在平面中， 和形成正交網路。可以通過一個保持 和正交性質的轉換將流動從平面轉換到另一個平面，比如說
平面。這一轉換稱為函式
的變換函式。
可以看出，一個平面中無限小的三角形可以在保持角度和相似性的條件下變換到平面中的一個相似的無限小三角形。這樣的轉換用於流動的變換；梅卡托投影就是將地球保角變換到一個平面上。如果知道簡單形狀的流型，我們就可以通過選擇合適的形式函式構築複雜形狀的流形。因此，通過方程我們能夠得到描述在平面中更複雜流動的
。
套用領域
滿足二元拉普拉斯方程的調和函式u可以看做是某解析函式的實部(或虛部)，因此，與拉普拉斯方程的解有關的實際問題，也可轉化為複變函數的問題。這也是複變函數套用的另一重要方面.。由於電流I是電荷流動的速度，類似於流體的速度，因此，與複變函數在流體力學中的套用相似，複變函數也可套用於電動力學。由於平面熱傳導問題溫度的定常分布滿足二元拉普拉斯方程，其解為調和函式，可看做解析函式的實部(或虛部)，所以複變函數可套用於熱傳導問題。
