正文,
正文
數學上規定複平面和複平面之間的變換=()是導數′()厵0的各點處是保角變換,它是求解二維電磁場問題的一種有力工具。例如兩個平行的柱形電極,當長度遠大於間距從而可以忽略柱體的末端效應時，就可近似為二維問題。保角變換可套用於：靜電、靜磁問題，包括傳輸線（即橫電磁場）問題；具有複雜邊界的導波系統問題；以及電磁場的反演問題。
靜電、靜磁問題的套用甚廣，在電源或磁源以外的區域，二維問題的電場強度或磁場強度等於某一靜勢函式的梯度，後者滿足二維拉普拉斯方程，其解稱為(圓)調和函式，記為(,)，則
設復變數=+j，則根據已知的(,),總可以找到另一個調和函式=(,)，構成解析函式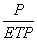
電磁場的保角變換
靜電、靜磁問題的套用甚廣，在電源或磁源以外的區域，二維問題的電場強度或磁場強度等於某一靜勢函式的梯度，後者滿足二維拉普拉斯方程，其解稱為(圓)調和函式，記為(,)，則
設復變數=+j，則根據已知的(,),總可以找到另一個調和函式=(,)，構成解析函式
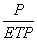電磁場的保角變換ω(z)=u+jv
z=x+jy
稱和為共軛函式,為復勢函式。可以證明也滿足二維拉普拉斯方程並且在複平面上的等值線是兩簇互相正交的曲線。若選其中的一簇為等勢線，則另一簇就代表力線（電力線、磁力線），相應地稱這兩簇曲線所對應的函式為勢函式和流函式（通量函式）。
電磁場的保角變換若能找到兩個共軛函式，其中一個函式的等值線恰好和所研究的電極邊界重合，則另一個函式的等值線即代表由電極發出的電力線。因而,根據電力線的流函式就可以計算出電極表面所帶的電荷量，從而可以計算場分布和電容量等。例如平板電容器二維邊緣場的分析（圖1a）。設兩極板的電位分別為±1伏，間距為2(長度單位)，置於-平面中(=+j)，根據對稱性，只需分析上半平面(>0)的場。利用解析函式
的保角變換(=+j)，使-平面上由點、、連成的多角形變換成以點′、′、′連線為界的上半－平面（圖1b）。已知後者的復勢函式為
故平板電容器的復勢函式滿足關係式
據此可得出在－平面內的等勢線（=常數）和電力線（=常數）的曲線方程。
某些邊界形狀較複雜的導波系統，經保角變換可變換成一個較易處理的簡單邊界形狀。例如利用波導的電磁場解描述溝槽形波導（圖2）的電磁場時就需要用保角變換。
電磁場的保角變換在電磁場反演問題中，由已知遠區場推算電磁場源的距離、方向和形狀時，可採用保角變換，將已知二維閉合曲線的外域變換成單位圓的外域，並利用變換函式以及遠區場兩者的勞倫茨級數展開式的係數關係，可以得出解的低頻估計。
在具體問題中，根據預給的勢函式或流函式，去尋找合適的共軛函式並不容易。對於場域具有多角形邊界的問題，施瓦茨變換是一種很有用的方法。它把一個複平面上由實軸和無限大的圓弧所圍成的上半平面變換到另一複平面上的多角形內域，或反之。對於除了平角和零角之外只含一、二個正角的多角形，施瓦茨變換是初等解析函式；當正角增加到三、四個，變換與橢圓積分及橢圓函式有關。橢圓函式屬於雙周期解析函式，常套用於分析帶狀線等特種截面傳輸線。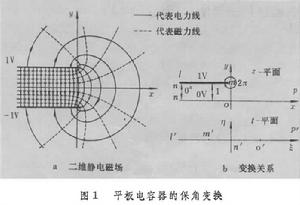
電磁場的保角變換
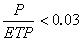電磁場的保角變換
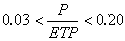電磁場的保角變換
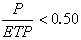電磁場的保角變換
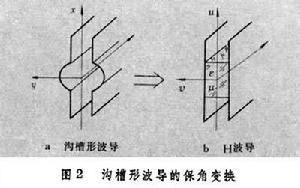電磁場的保角變換
電磁場的保角變換若能找到兩個共軛函式，其中一個函式的等值線恰好和所研究的電極邊界重合，則另一個函式的等值線即代表由電極發出的電力線。因而,根據電力線的流函式就可以計算出電極表面所帶的電荷量，從而可以計算場分布和電容量等。例如平板電容器二維邊緣場的分析（圖1a）。設兩極板的電位分別為±1伏，間距為2(長度單位)，置於-平面中(=+j)，根據對稱性，只需分析上半平面(>0)的場。利用解析函式
的保角變換(=+j)，使-平面上由點、、連成的多角形變換成以點′、′、′連線為界的上半－平面（圖1b）。已知後者的復勢函式為
故平板電容器的復勢函式滿足關係式
據此可得出在－平面內的等勢線（=常數）和電力線（=常數）的曲線方程。
某些邊界形狀較複雜的導波系統，經保角變換可變換成一個較易處理的簡單邊界形狀。例如利用波導的電磁場解描述溝槽形波導（圖2）的電磁場時就需要用保角變換。
電磁場的保角變換在電磁場反演問題中，由已知遠區場推算電磁場源的距離、方向和形狀時，可採用保角變換，將已知二維閉合曲線的外域變換成單位圓的外域，並利用變換函式以及遠區場兩者的勞倫茨級數展開式的係數關係，可以得出解的低頻估計。
在具體問題中，根據預給的勢函式或流函式，去尋找合適的共軛函式並不容易。對於場域具有多角形邊界的問題，施瓦茨變換是一種很有用的方法。它把一個複平面上由實軸和無限大的圓弧所圍成的上半平面變換到另一複平面上的多角形內域，或反之。對於除了平角和零角之外只含一、二個正角的多角形，施瓦茨變換是初等解析函式；當正角增加到三、四個，變換與橢圓積分及橢圓函式有關。橢圓函式屬於雙周期解析函式，常套用於分析帶狀線等特種截面傳輸線。
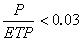電磁場的保角變換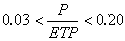電磁場的保角變換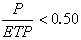電磁場的保角變換電磁場的保角變換電磁場的保角變換