克里斯托菲爾-施瓦茲公式

克里斯托菲爾-施瓦茲公式是多角形區域共形映射函式的表達式。

基本介紹

• 中文名：克里斯托菲爾-施瓦茲公式
• 外文名：Christoffel-Schwarz formula
• 適用範圍：數理科學

簡介

克里斯托菲爾-施瓦茲公式是多角形區域共形映射函式的表達式。

設w=f(z)是將上半平面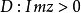共形映射到多角形區域G的單葉解析函式，z平面實軸上的n個點a₁,a₂,...,a_n(-∞<a₁<a₂<...<a_n<+∞)對應於w平面上多角形區域G的頂點w₁,w₂,...,w_n；λ₁π,λ₂π,...,λ_nπ(0<λ_j<2,j=1,2,...,n)表示G在頂點w₁,w₂,...,w_n處的內角，則有克里斯托菲爾-施瓦茲公式

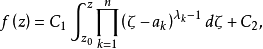其中，C₁，C₂是兩個復常數，z₀∈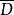，z₀≠∞。

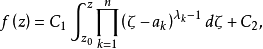
共形映射

共形映射是複變函數論的一個分支，它從幾何的觀點來研究複變函數，其通過一個解析函式把一個區域映射到另一個區域進行研究。這個性質可以將一些不規則或者不好用數學公式表達的區域邊界映射成規則的或已成熟的區域邊界。

數學上，一個共形變換（保角變換）是一個保持角度不變的映射。

解析函式

解析函式是區域上處處可微分的複函數。17世紀，L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數，且滿足微分方程組，並指出f(z)=Φ(x,y)+iΨ(x,y)是可微函式，這一命題的逆命題也成立。

柯西把區域上處處可微的複函數稱為單演函式，後人又把它們稱為全純函式、解析函式。B.黎曼從這一定義出發對複函數的微分作了深入的研究，後來，就把上述的偏微分方程組稱為柯西-黎曼方程，或柯西-黎曼條件。