基本介紹
- 中文名:邊界對應定理
- 外文名:theorem of boundary correspondence
- 屬性:複變函數幾何理論的基本定理之一
- 所屬學科:數學
- 所屬問題:複變函數論(幾何函式論)
- 相關概念:共形映射,有界單連通區域等
基本介紹








邊界對應定理的逆定理
















































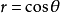


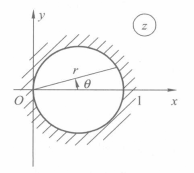 圖1(a)
圖1(a)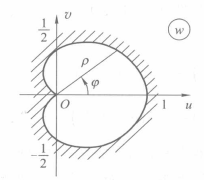 圖1(b)
圖1(b)
























































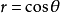


 圖1(a)
圖1(a) 圖1(b)
圖1(b)邊界對應定理(theorem of boundary correspondence)是複變函數幾何理論的基本定理之一。設z平面上單連通區域D的邊界是一條閉簡單連續曲線C,設單葉函式w=f(z)把D...
體所對應的多項式族的穩定性可由其相對邊界(相對於仿射包的邊界)所對應的多項式...原象定理是關於多項式係數空間中幾何體的穩定性的另一個判別定理.對於多項式族屍...
邊界層定理是當流體在大雷諾數條件下運動時,可把流體的粘性和導熱看成集中作用在流體表面的薄層即邊界層內。根據邊界層的這一特點,簡化納維-斯托克斯方程,並加以...
G的素端的全體稱為G的卡拉西奧多裡邊界,簡稱卡氏邊界。早在1913年,卡拉西奧多...值分布論,簡化了在單位圓上單連通域的保形變換的主要定理,給出了邊界對應的...
羅伯津斯基定理的一個套用是說明要素積累對生產可能性邊界的影響效果。羅伯津斯基定理封閉條件下 要素稟賦增加之後,生產可能性邊界的兩個端點所分別對應的X、Y的最大產...
(黎曼映射定理)若 為單連通區域,其邊界多於一點, 為 中任意一點,則在上存在唯一的一個一個把意義對應地映射成單位圓內部的共形映射 ,且 。...
對應可以達到的期望收益,有效集上的組合有最小的方差;而對應同一個方差,有效集...分離定理兩基金分離定理 編輯 在所有有風險資產組合的有效組合邊界上,任意兩個...
拋物型方程初一邊值問題的重要性 質,亦即方程的解在達到最大值的邊界上的外法...· 這就是霍普夫型邊界點定理.此論斷與橢圓型方程 的相應結論是一致的,但x}x...
霍普夫邊界點定理(Hopf boundary point theo- rem)有關二階橢圓型方程的一個重要性質.這類 方程(或不等式)的非常數解在達到最大值的邊界點 上的外法嚮導數必...
與電荷位置對應的電通量 注意到 在x=0處非連續,如圖2所示。因而可用單位階躍函式...也就是說,在穩恆電流情況下,對於以閉合迴路為邊界的所有曲面而言,安培環路定理...
在數論中,狄利克雷定理說明對於任意互質的正整數a,...1837年他提出函式是x與y之間的一種對應關係的現代...關位勢理論的文章,論及著名的第一邊界值問題,現稱...
經典的法圖定理斷言:Rn的球內的正調和函式在邊界上幾乎處處有非切向邊界值。... 經典的法圖定理斷言:Rn的球內的正調和函式在邊界上幾乎處處有非切向邊界值。...
亨特-惠登定理是函式在某點的非切向邊界值與半細邊界值之間的關係的定理。... 邊界值與半細邊界值之間的關係的定理。...對應一個局部坐標系(X,y),X∈Rn-1...
卡拉西奧多里證明了邊界對應定理,即在黎曼映射定理的條件下 ,若бD= L是一條簡單閉曲線,則映射函式f(Z) 可以連續開拓到L上且實現L與|w|=1之間的雙方單值...
定理二(保域性)解析函式(不恆為常數)把區域映射為區域。定理三(邊界對應原理)設區域 D的邊界為簡單閉曲線C,w=f(z)在 上解析,則將C一一映射為區域G的邊界 ...
4.關於共形映射的黎曼存在定理和邊界對應定理第七章習題第八章解析延拓1.解析延拓的概念與冪級數延拓2.透弧解析延拓、對稱原理3.完全解析函式及黎曼面的概念...
4.關於共形映射的黎曼存在定理和邊界對應定理第七章習題第八章解析延拓1.解析延拓的概念與冪級數延拓2.透弧解析延拓、對稱原理3.完全解析函式及黎曼面的概念...
7.4 保形映射的黎曼存在定理與邊界對應定理7.5 若干個值分布研究中的不等式*習題7參考文獻 [1] 參考資料 1. 0 [引用日期2016-07-06] 詞條標籤: 文化 ...
一、黎曼存在定理二、黎曼邊界對應定理習題六第七章 解析延拓簡介1 解析延拓的概念和方法一、基本概念二、冪級數延拓三、透弧延拓2 完全解析函式及單值性定理...
4.關於共形映射的黎曼存在定理和邊界對應定理第七章習題第八章解析延拓1.解析延拓的概念與冪級數延拓2.透弧解析延拓、對稱原理3.完全解析函式及黎曼面的概念...
13.3邊界對應定理及唯一性定理13.4擬共形映射的Holder連續性13.5擬共形延拓13.6擬共形映射的Riemann映射定理13.7全平面上具有給定復特徵的擬共形映射的存在性...
(n)在緊集K上的模可以用f在K的鄰域上的模來控制這一事實,使證明得以簡化,而且上述事實在別處還要用到.其他如邊界對應定理和Weierstrass因子分解定理的證明,與...
40.黎曼定理13.邊界對應和對稱原理41.邊界的對應42.對稱原理43.關於橢圓函式的概念44.模函式和皮卡定理習題第五章解析方法14.整函式與亞純函式的分解...
第一章 riemann映射定理§1 解析映射§2 解析函式序列與正規族§3 riemann映射定理的證明§4 共形映射的邊界對應§5 模函式§6 單值性定理...
*附錄二 若爾當定理*附錄三 同調及同倫形式的柯西定理*附錄四 整函式的無窮乘積展式及亞純函式的*附錄五 黎曼映射定理及邊界對應定理的證明...
復積分和柯西積分定理,級數理論,留數與輻角原理,許瓦茲原理、開映射原理、最大模原理、黎曼邊界對應原理,共形映射理論,解析開拓、調和函式、正規族、畢伯巴赫猜想...
2黎曼存在定理 2.1Montel定理 2.2黎曼存在定理 3邊界對應 3.1函式g(w)的連續開拓 3.2函式f(z)的連續開拓 4多角形的共形映射 4.1Schwarz—Christoffel公式 4.2...
通過取倒數,可以得到對應的最小模原理。後者聲稱如果...那么函式 |f(z)| 的最小值只會在D的邊界上取...用於證明代數基本定理:使用最大模原理的證明是一個...
流動現象的幾何條件(流場的邊界形狀和尺寸)、物性條件(流體密度、粘性等)、邊界...從更具有普遍意義的相似定理來看,兩個流動相似,則相似準則數對應相等,由Π定理...
