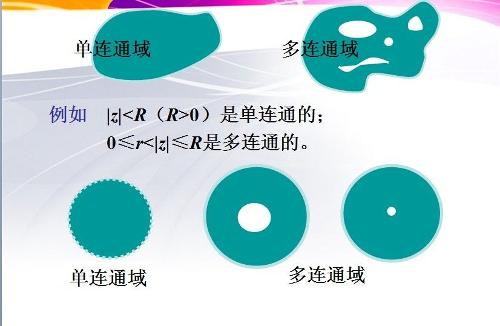
設D是一區域,若屬於D內任一簡單閉曲線的內部都屬於D,則稱D為單連通區域,單連通區域也可以這樣描述:D內任一封閉曲線所圍成的區域內只含有D中的點。更通俗地說,單連通區域是沒有“洞”的區域。
基本介紹
- 中文名:單連通區域
- 外文名:simply connected domain
- 所屬學科:數學
- 特點:沒有“洞”的區域
- 相關概念:簡單閉曲線、圍線、多連通區域等
基礎知識





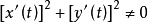
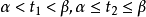


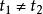



 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖2(a)
圖2(a) 圖2(b)
圖2(b)單連通區域的一些性質


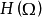











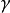
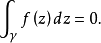


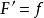






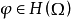
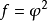






單連通區域內的柯西積分定理
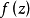
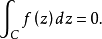
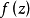
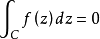
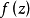
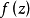
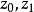




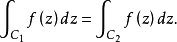
設D是一區域,若屬於D內任一簡單閉曲線的內部都屬於D,則稱D為單連通區域,單連通區域也可以這樣描述:D內任一封閉曲線所圍成的區域內只含有D中的點。更通俗地說,單連通區域是沒有“洞”的區域。





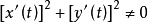


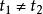



 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖2(a)
圖2(a) 圖2(b)
圖2(b)

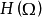











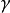
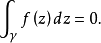


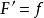






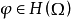
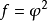






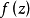
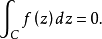
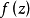
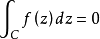
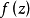
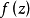
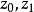




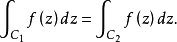
設D是一區域,若屬於D內任一簡單閉曲線的內部都屬於D,則稱D為單連通區域,單連通區域也可以這樣描述:D內任一封閉曲線所圍成的區域內只含有D中的點。更通俗地...
單連通域是直觀上沒有洞的平面區域的推廣,即區域內任何一條簡單閉曲線的內部沒有不屬於D的點。...
複平面上的一個區域G,如果在其中任做一條簡單閉曲線,而閉曲線的內部總屬於G,就稱G為單連通區域。一個區域如果不是單連通區域,就稱為多連通區域。...
斯米爾諾夫區域是一種與多項式系完備性相關的區域。設G是有界單連通區域,其邊界曲線C是若爾當可求長曲線,z=Ψ(ω)是將|ω|<1映射到G且在ω=0點規格化的保...
邊界對應定理(theorem of boundary correspondence)是複變函數幾何理論的基本定理之一。設z平面上單連通區域D的邊界是一條閉簡單連續曲線C,設單葉函式w=f(z)把D...
當D為單連通區域時,如果以D內沿以a為起點的所有曲線都可以解析開拓,則f(z)在D內由P(z;a)確定的分支是單值的,這便是單值性定理。...
。直觀地說,單連通區域是沒有空間的區域,否則稱為復連通區域。 當xOy平面上的曲線起點與終點重合時,則稱曲線為閉曲線。設平面的閉曲線L圍成平面區域D,並規定當...
擴充複平面上的一個區域D稱為單連通區域,若屬於D的任意一條簡單閉曲線的內部或外部之一仍屬於D,否則就稱為多連通區域。複平面及擴充複平面本身就都是單連通區域...
在數學中, 黎曼映射定理是複分析最深刻的定理之一,也是複變函數幾何理論最基本、最重要的定理,此定理分類了C的單連通開子集。...
(1)平面上的單連通區域與復連通區域設 是平面 上的區域。如果 內的任何封閉曲線 所圍成的區域 ,恆有 ,則 稱為單連通區域;否則, 稱為復連通區域。...
只含有一個自變數的複變函數稱為單複變函數(function of a complex variable),...平面上的一個單連通區域,它的邊界多於一點, 為 內一點並且 為一實數,則存在...
.於是,複平面以 為其唯一的邊界點;擴充複平面以 為內點,且它是唯一的無邊界的區域.(2)單連通的概念也可推廣到擴充複平面上的區域上.對擴充複平面上的區域D...
單葉函式是複變函數中一類重要的解析函式。對複平面區域D上單值的解析函式ƒ(z),若對D中任意的不同的兩點z1、z2有ƒ(z1)≠ƒ(z2),則說f(z)為D...
該定理的一個直接推論,是在單連通域內全純函式的路徑積分可以用類似於微積分基本定理的方法來計算:設 是複平面的一個開子集。 是一個 上的全純函式。函式f在...
若拓撲空間T為曲面S且S\G的每個連通片都是單連通區域,則稱G為曲面S上的地圖,記為M.用G(M)表示由M的頂點和邊所構成的圖。地圖M的可定向性是由曲面S的可...
在單連通空間內,無旋矢量場具有路徑無關的性質。這是因為無旋矢量場是保守的,而保守矢量場又是路徑無關的。這個結果也可以從斯托克斯定理直接推出。在連通區域內,...
設D(D⊂C)是單連通區域,且其內部含有原點O。若共形映射ω=φ(z)將D映成{ω||ω|<R0},並使φ(0),|φ'(0)|=1,則稱R0=R0(D)為D關於0的內映射...
如果函式f(z)在區域D內連續,並且沿著D內任何一條可求長閉曲線γ的積分,那么...若D是複平面C上的個單連通區域,f(z)在D內是解析的,γ是D內的一條可求長...
若拓撲空間T為曲面S且S\G的每個連通片都是單連通區域,則稱G為曲面S上的地圖,記為M。用G(M)表示由M的頂點和邊所構成的圖,地圖M的可定向性是由曲面S的可...
保形映射的基本定理是黎曼映射存在唯一性定理,它斷言:若D 是一個邊界點集多於一個點的單連通區域,Z0∈D ,則一定存在唯一確定的解析函式w=f(Z)將D雙方單值保...
最簡單的柯西積分定理的形式為:當D是單連通區域 ,而f(z)是D上的解析函式時,以下3個互相等價的結論成立 :① f(z) 在D內沿任意可求長曲線積分與路徑無關。...
為單連通域D內的個解析函式, 為D內一點,環路C為D內包圍 的一條簡單閉曲線,由單連通域柯西定理可知,.現在考慮積分,顯然函式 在 處不解析,所以積分 一般不為...
1910年,布勞威爾發現了平面上不可分解的連續統是可數個單連通區域的公共邊界.1912年,他證明了可以把約當曲線定理推廣到n維空間.1913年,他給出了拓撲空間維數的嚴格...
通常定義為:若環線所包含的面積始終在環線的左側,即環線所圍面積為單連通區域時的逆時針方向,稱環線的正方向,此時環流值大於0。如圖1(a)中所示,在大氣環流中...
定理一(黎曼定理)對邊界多於一點的任意兩個單連通域 D和 G,對任意給定的實數點 及 , 總唯一存在把D一一映射為G的 ,使得 , 。定理二(保域性)解析函式(不...
在區域D內全純的函式,能以D的任一點為中心展開為冪級數,這些冪級數(函式元素)的集合,成為一個解析函式的分支.當D為單連通區域時,如果以D內的點a為中心的...
若拓撲空間𝓘為曲面S且S\G的每個連通片都是單連通區域,則稱G為曲面S上的地圖,記為M。用G(M)表示由M的頂點和邊所構成的圖。...
稱為f的原函式或純量勢函式.當f連續時,f為勢場若且唯若它是保守場;當.f=(f} }fZ,..., f,})連續可微且其定義域為R”的單連通域時,f是勢場當且...
