斯米爾諾夫區域是一種與多項式系完備性相關的區域。使多項式系在Ep(G)中完備的充分必要條件是,區域G為斯米爾諾夫區域。
基本介紹
- 中文名:斯米爾諾夫區域
- 外文名:Smirnov domain
- 適用範圍:數理科學
簡介,性質,完備性,
簡介
斯米爾諾夫區域是一種與多項式系完備性相關的區域。
設G是有界單連通區域,其邊界曲線C是若爾當可求長曲線,z=Ψ(ω)是將|ω|<1映射到G且在ω=0點規格化的保角映射,ω=φ(z)為其逆映射,設ρ>0,Ep(G)={f(z)|f(z)在G內解析,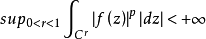 },其中Cr是C的內等勢線。若ψ(ω)滿足
},其中Cr是C的內等勢線。若ψ(ω)滿足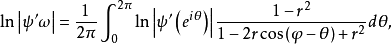 其中ω=reiθ,0≤r<1,則稱G為斯米爾諾夫區域。
其中ω=reiθ,0≤r<1,則稱G為斯米爾諾夫區域。
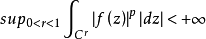
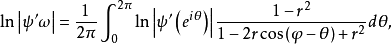
性質
使多項式系在Ep(G)中完備的充分必要條件是,區域G為斯米爾諾夫區域。
當p=2時,這個定理首先是由斯米爾諾夫證明的,後來克爾德什與拉夫連季耶夫把它推廣到一般的p>0。
完備性
是指在數學及其相關領域中,當一個對象具有完備性,即它不需要添加任何其他元素,這個對象也可稱為完備的或完全的。
完備性也稱完全性,可以從多個不同的角度來精確描述這個定義,同時可以引入完備化這個概念。完備性在一般空間中表示任何空間中的柯西點列的一致收斂極限包含於這個空間中。完備性與所定義的度量有關,一旦定義了度量,那么可以討論這個空間的完備性。
