基本介紹
- 中文名:保角映射
- 外文名:conformal mapping
- 領域:數學
- 映射性質:保角性,伸縮率不變性
- 條件:在區域內處處解析
- 套用領域:流體力學、空氣動力學、電學等
概念
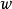
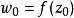
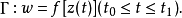
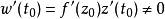
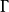
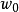


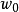
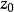
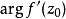

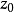
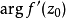
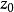
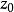
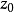
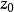
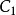
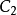
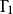

 圖1
圖1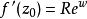
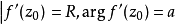



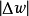
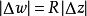
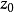
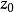
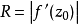


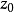
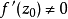



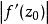
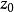

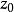

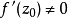
幾種簡單的保角映射

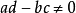
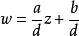
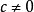
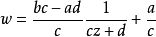
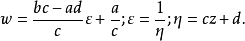
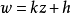

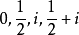
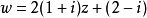

 圖2
圖2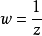

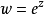



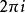
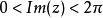
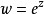
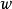
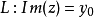

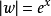
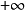
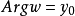


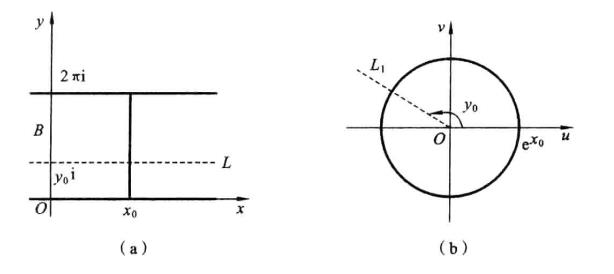 圖3
圖3
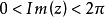
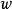



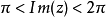
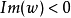
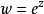
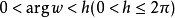
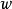

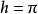
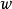
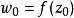
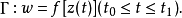
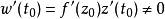
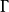
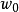


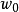
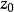
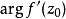

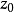
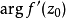
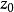
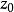
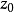
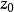
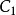
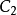
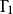

 圖1
圖1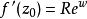
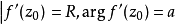



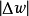
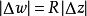
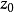
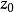
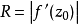


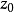
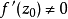



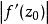
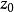

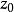

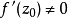

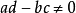
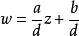
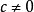
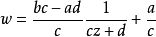
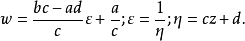
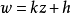

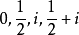
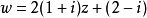

 圖2
圖2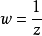

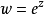



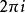
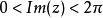
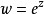
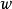
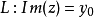

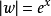
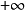
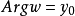


 圖3
圖3
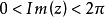
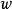



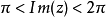
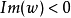
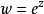
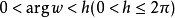
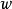

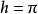
保角映射是複變函數最重要的概念之一,它可以將比較複雜的區域上的問題轉化到比較簡單的區域上進行研究。成功地解決了流體力學、空氣動力學、彈性力學、電學等學科中...
大學數學教程(第2卷第3冊)積分變換、數理方程、保角映射,是大學高等數學學習的一本教程。也可作為數學物理方法課程的補充教材或教學參考書用。...
保角對應(conformal correspondence)保持角度不變的一種對應.若在兩個曲面的點之間建立一一對應,使任意兩條曲線的交角在對應下保持不變,則此種對應稱為保角對應,...
設C是若爾當區域G的邊界曲線,z=Ψ(w)是將{w|w|>1}映射到C的外部且在∞處規格化的保角映射,f(z)在G內解析,在Ḡ上連續,則稱σn為f(z)的費伯係數...
許立忠.保角映射法精確求解漸開線齒輪齒根應力. 工程力學(EI收錄). 1/1999. 許立忠.超環面行星蝸桿傳動嚙合特性研究(EI收錄).農業機械學報.1997.28(4) 許立忠....
接著,L.Ahlfors利用關於帶形域的畸變定理,導出了角微商存在的充分必要條件,Wolff在保角映射的疊代的研究中套用了角微商 [2] 。...
在複變函數中,保角映射在理論和套用上都十分重要,而具有保角性和伸縮率不變性的映射即為保角映射,將此概念推廣到無窮維空間,特給出如下定義:設 為線性運算元,...
第28章jacobi保角映射28.1再談圓函式和橢圓函式28.2jacobi橢圓函式的保角映射第29章jacobi濾波器29.1jacobi橢圓函式的雙周期29.2jacobi橢圓函式逼近...
他發展了狄利克雷原理,並將其套用於保角映射、數學物理方程的邊值問題,把邊值問題的解化為二次函式的極值函式。他還系統地研究了邊值問題的特徵函式與特徵值的...
“複變函數”和“積分變換”2篇,全書分8章,內容包括:複數和複變函數;解析函式;複變函數的積分;解析函式的級數展開;留數及其套用;保角映射;傅立葉變換;拉普拉斯...
第六章 保角映射第七章 拉普拉斯變換附錄Ⅰ 留數公示表附錄Ⅱ 某些定積分的計算公式附錄Ⅲ 拉氏變換主要公示表附錄Ⅳ 拉氏變換簡表...
1960年前後,他和莊圻泰在北京大學數學力學系一起領導了廣義解析函式、擬保角映射及其套用的新方向的研究,為我國在這些分支方面的研究奠定基礎、培養人才做出了貢獻。...
因此當n≥2時,它在全平面除z=0以外到處實現共形映射(保角映射)。它將圓周|z|= r變為圓周|w|=rn,將射線argz=θ變為射線argw=nθ。任何一個區域,只要...
《電磁場分析中的套用數學》介紹電磁場分析中的相關數學知識,內容包括矢量和並矢的微積分、複變函數的解析延拓、г函式、保角映射法求解平面靜電場、超幾何微分方程...
映射法可分為三大類 :保角映射法、基於偏微分方程法、代數插值法。三維格線劃分的許多方法都是先將形體的表面離散化,所以曲面映射是三維映射的基礎。在空間參數...
本書系統地介紹了許瓦茲引理、保角映射以及複函數的逼近。 並且著重地介紹了Carathéodory和Kobayashi度量及其在複分析中的套用。 論述深入淺出,簡明生動,讀後有益於...
劉殿魁教授1937年出生 先後師從錢令希院士、劉恢先院士,現任中國力學學會固體力學專業委員會委員,首創分析彈性波散射與動應力集中的複變函數與保角映射方法,是經典...
很多平面問題利用複變函數和保角映射可以求得解析解,這是經典流體力學的重要內容。但對幾何形狀比較複雜的物體,必須用下述的數值解法。...
將舊坐標 z 和新坐標都作為復變數﹐它們之間的關係用保角映射z =f ()表示。自變數t 變換成s 的關係是dt /ds =|dz /d|。這些變換中最著名的是蒂勒變換z...
G.R.基爾霍夫於1867年,H.von亥姆霍茲於1868年為計算與物體尾流相關的阻力所提出的複變函數保角映射方法奠定了自由流線理論或空泡流理論的數學基礎。由於空泡形狀...
設G是有界單連通區域,其邊界曲線C是若爾當可求長曲線,z=Ψ(ω)是將|ω|<1映射到G且在ω=0點規格化的保角映射,ω=φ(z)為其逆映射,設ρ>0,Ep(G)=...
設K是複平面上的緊集,其邊界曲線C是若爾當曲線或若爾當弧,z=Ψ(w)是將|w|>1映射到K的余集且在∞點規格化的保角映射,則稱節點 為K上的n+1個費耶爾...
9.1 保角映射9.2 全純矢量函式的邊值問題9.3 具有橢圓孔的全平面之拉伸9.4 剛性線第三章 軸對稱問題§1 軸對稱共軛調和函式§2 軸對稱問題的B-G解和P-N解...
發展狄利克雷原理,並把它套用於保角映射和橢圓型方程的邊值問題。對邊值問題中的特徵值和特徵函式作了出色的研究。柯朗於1972年1月27日在紐約市去世...
