基本介紹
- 中文名:旋轉矩陣
- 外文名:Rotation matrix
- 學科:數學
- 研究者:底特羅夫
- 分為:主動旋轉與被動旋轉
- 相關術語:正交矩陣
簡介
歷史
性質


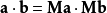



二維空間

三維空間
旋轉
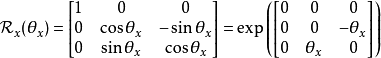



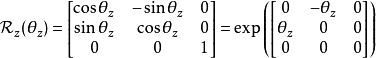


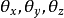




角-軸表示




歐拉角表示



SVD表示
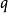
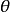

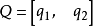





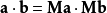




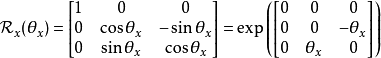



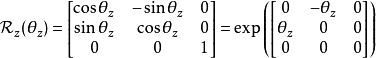


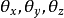











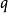
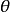

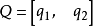


旋轉矩陣(英語:Rotation matrix)是在乘以一個向量的時候有改變向量的方向但不改變大小的效果並保持了手性的矩陣。旋轉矩陣不包括點反演,點反演可以改變手性,也就是...
跳轉至: 導航、 搜尋 在運動學裡,歐拉旋轉定理(Euler's rotation theorem)表明,在三維空間裡,假設一個剛體在做一個位移的時候,剛體內部至少有一點固定不動,則...
變換矩陣是數學線性代數中的一個概念。線上性代數中,線性變換能夠用矩陣表示。如果T是一個把Rn映射到Rm的線性變換,且x是一個具有n個元素的列向量 ,那么我們把m...
定義設矩陣P(i,j)是與單位矩陣只在(i,i),(i,j),(j,i),(j,j)四個位置上元素不同的矩陣,其中(i,i)和(j,j) 位置上元素為cosθ, (i,j) 位置上...
旋轉矩陣是彩票組號的最科學、最有效的方法,你只需在本投注卡中選擇你所需要的類型,輕鬆運用旋轉矩陣進行彩票的投注和對獎。...
《足球彩票旋轉矩陣》作者李相春,中國物價出版社出版。...... 本書向讀者介紹了全部適用於手工操作的足彩旋轉矩陣,並提供了切實可行的使用方法.為減小讀者工作量,隨...
在運動學裡,歐拉旋轉定理(Euler's rotation theorem)表明,在三維空間裡,假設一個剛體在做一個位移的時候,剛體內部至少有一點固定不動,則此位移等價於一個繞著...
中文名稱 軸旋轉矩陣 英文名稱 axis rotation matrix 定義 用繞某一軸線的轉動來描述構件在三維空間中有限轉動的矩陣。 套用學科 機械工程(一級學科),機構學(...
《手把手教你玩彩票·組號VS旋轉矩陣》是2004年中國物價出版社出版的圖書,由彩天使編輯部編著。...
《雙色球旋轉矩陣投注卡大全》共有六冊,分別是:雙色球旋轉矩陣投注卡大全使用手冊、雙色球平衡式旋轉矩陣投注卡、雙色球1膽型旋轉矩陣投注卡、雙色球2膽型旋轉...
羅德里格旋轉公式是計算三維空間中,一個向量繞旋轉軸旋轉給定角度以後得到的新向量的計算公式。這個公式使用原向量,旋轉軸及它們叉積作為標架表示出旋轉以後的向量。...
《彩票組號經典—旋轉矩陣》一書的升級版在前一版本地基礎上進行了較大的改動和最佳化,隨書附送的軟體WheelStar也由1.0版本升級為2.0版本,功能進一步增強,使用的...
旋轉矩陣的原理在數學上被稱為“覆蓋設計”,是一個看似簡單實際卻異常複雜的問題,至今還有許多難題沒有解決。...
《旋轉矩陣3.0彩票組號經典》的作者是李相春,中國市場出版社出版...... 《旋轉矩陣3.0彩票組號經典(附光碟)》及配套軟體Wheelstar3.秉承“以人為本”的設計理念,緊...
方差最大化旋轉是在主成分分析或因子分析中使用的一種方法,通過坐標變換使各個因子載荷的方差之和最大。通俗地說,就是(a)任何一個變數只在一個因子上有高貢獻...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
一款完全免費的彩票軟體!用於'福彩雙色球',全國各種'選5型','選7型'彩票的旋轉矩陣縮水。其意義在於,如果你所選擇的多個號碼中包括了開獎的號碼,那么你只要用...
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
《雙色球旋轉矩陣投注卡大使用手冊(共6冊)》是2009-11年中國市場出版社出版的圖書,作者是彩天使。...
Denavit 和Hartenberg在1955年提出一種通用的方法,這種方法在機器人的每個連桿上都固定一個坐標系,然後用4×4的齊次變換矩陣來描述相鄰兩連桿的空間關係。通過依次...
在計算機視覺中,基礎矩陣(Fundamental matrix)F是一個3×3的矩陣,表達了立體像對的像點之間的對應關係。...
《矩陣理論與方法》是2006年電子工業出版社出版的圖書,作者是吳昌愨,魏洪增。...... 3.2矩陣的qr分解3.2.1矩陣的qr分解3.2.2用初等旋轉矩陣求矩陣的qr分解...
現在我們用矩陣形式寫出基向量和基,這樣的矩陣我們叫它基矩陣。...... 坐標系中的一個點,如果要它圍繞該坐標系中一個坐標軸旋轉,就給它的坐標值乘相應的旋轉矩...
glRotated 函式將相乘旋轉矩陣的當前的矩陣。...... glRotated 函式將相乘旋轉矩陣的當前的矩陣。語法void WINAPI glRotated(GLdouble angle,GLdouble x,...
式中R、Z'、N、Z是轉動運算元,並可用矩陣表示如下:在進行轉動運算元的乘法運算時...歐拉角在SO(3)上,形成了一個坐標卡(chart) ;SO(3)是在三維空間裡的旋轉的...
