基本介紹
- 中文名:單位向量
- 外文名:Unit Vector
- 學科:數學
- 類型:數學術語
- 特點:模等於1的向量
- 向量:具有大小和方向的一個量
向量
定義
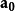
性質
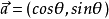

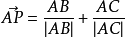

例題





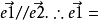
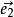


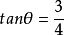
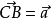
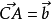





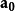
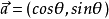

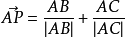






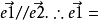
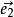


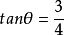
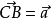
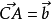




單位向量是指模等於1的向量。由於是非零向量,單位向量具有確定的方向。單位向量有無數個。一個非零向量除以它的模,可得所需單位向量。一個單位向量的平面直角坐標...
線上性代數中,列向量是一個 n×1 的矩陣,即矩陣由一個含有n個元素的列所組成:列向量的轉置是一個行向量,反之亦然。所有的列向量的集合形成一個向量空間,它...
平面向量是在二維平面內既有方向(direction)又有大小(magnitude)的量,物理學中也稱作矢量,與之相對的是只有大小、沒有方向的數量(標量)。平面向量用a,b,c上面...
向量的向量積是一個向量,其大小為aXb=|a|X|b|sin《a,b》,方向用右手法則確定。...... 這個定義有個問題,就是同時有兩個單位向量都垂直於和:若滿足垂直的條...
n元向量(n-tuple vector)亦稱n維向量,是通常向量(矢量)的推廣,設P為域,n是正整數,P中n個元素構成的有序組(a1,a2,…,an)稱為P上的n元向量,ai(i=1,2...
向量積,數學中又稱外積、叉積,物理中稱矢積、叉乘,是一種在向量空間中向量的二元運算。與點積不同,它的運算結果是一個向量而不是一個標量。並且兩個向量的叉...
矩陣的特徵向量是矩陣理論上的重要概念之一,它有著廣泛的套用。數學上,線性變換的特徵向量(本徵向量)是一個非簡併的向量,其方向在該變換下不變。該向量在此...
1806年,瑞士人阿爾岡以表示一個有向線段或向量(vectors)。麥比烏斯(1827年)則以AB表示一起點為A而終點為B的向量,這用法為相當廣泛的數學家所接受。實際上,現在...
與向量相對的概念稱標量或數量,即只有大小、絕大多數情況下沒有方向(電流是特例)、不滿足平行四邊形法則的量。向量的大小是相對的,在有需要時,會規定單位向量,以...
在向量微積分中,弗萊納公式(Frenet–Serret 公式)用來描述歐幾里得空間R中的粒子在連續可微曲線上的運動。更具體的說,弗萊納公式描述了曲線的切向,法向,副法方向...
