基本介紹
- 中文名:非零向量
- 外文名:nonzero vector
- 解釋:長度不為0的向量
- 學科:數理科學
- 類型:數學術語
- 向量:指具有大小和方向的量
向量
向量的模
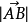
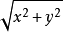
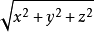
零向量
定義
性質
相關拓展
說單位向量有多少個?有無數個,任意方向都有一個單位向量.

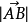
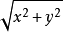
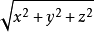
非零向量長度是指向量的大小(向量的長度/向量的模)不為零的向量。在數學中,向量(也稱為歐幾里得向量、幾何向量、矢量),指具有大小(magnitude)和方向的量。它可以...
長度為零的向量是零向量,也即模等於零的向量,記作0。注意零向量的方向是無法確定的。但我們規定:零向量的方向與任一向量平行,與任意向量共線,與任意向量垂直。...
非零矩陣中所含元素不全為零,即其為至少有一個元素不為零的矩陣,也就至少存在一個一階行列式的值非零。所以非零矩陣的秩r≥1...
平行向量,也叫共線向量。是指方向相同或相反的非零向量。非零向量與任意向量平行。...... 平行向量:也叫共線向量,方向相同或相反的非零向量。相等向量:長度相等...
設W為向量空間 V 的一個非空子集,若W在 V 的加法及標量乘法下是封閉的,且零向量0∈ W,就稱W為 V 的線性子空間。給出一個向量集合 B,那么包含它的最...
在平面幾何中可以表示任意向量a的兩個非零向量e1、e2稱為平面向量基底(Plane vector basis),表示為a=xe1+ye2,用基底e1、e2表示向量a時,實數x、y的取值是唯一...
矩陣的特徵向量是矩陣理論上的重要概念之一,它有著廣泛的套用。數學上,線性變換的特徵向量(本徵向量)是一個非簡併的向量,其方向在該變換下不變。該向量在此...
方向向量(direction vector)是一個數學概念,空間直線的方向用一個與該直線平行的非零向量來表示,該向量稱為這條直線的一個方向向量。...
減法的方法:將兩個向量平移至公共起點,以向量的兩條邊作平行四邊形,結果由減向量的終點指向被減向量的終點(平行四邊形定則只適用於兩個非零非共線向量的加減) ...
此外,當這個齊次線性方程組的係數矩陣是一個方陣時,這個係數矩陣存在行列式為0,即有非零解,從而 線性相關。 注意 對於任一向量組而言,,不是線性無關的就是...
特徵值是線性代數中的一個重要概念。在數學、物理學、化學、計算機等領域有著廣泛的套用。設 A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,...
所以任何解都可以表示為一個零空間中的向量加上特定解y。如果一個線性映射A是單同態,則它的零空間是零。因為如果反過來它的零空間是非零,由類似上面的方法可以...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
(1)廣義定義:設M是n階方陣,如果對任何非零向量z,都有zTMz> 0,其中zT 表示z的轉置,就稱M為正定矩陣。例如:B為n階矩陣,E為單位矩陣,a為正實數。在a充分...
