方向向量

方向向量（direction vector）是一個數學概念，空間直線的方向用一個與該直線平行的非零向量來表示，該向量稱為這條直線的一個方向向量。

基本介紹

• 中文名：方向向量
• 外文名：direction vector
• 學科：數學
• 套用領域：解析幾何
• 相關：向量
• 作用：表示空間直線的方向

簡介

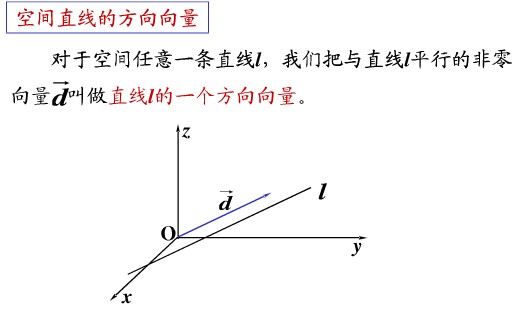
空間直線的方向用一個與該直線平行的非零向量來表示，該向量稱為這條直線的一個方向向量。直線在空間中的位置， 由它經過的空間一點及它的一個方向向量完全確定。

已知定點P₀（x₀,y₀,z₀)及非零向量v={l,m,n}，則經過點Pο且與v平行的直線L就被確定下來，因此，點P₀與v是確定直線L的兩個要素，v稱為L的方向向量。

由於對向量的模長沒有要求，所以每條直線的方向向量都有無數個。直線上任一向量都平行於該直線的方向向量。

方向向量的求解

只要給定直線，便可構造兩個方向向量（以原點為起點）。

（1）即已知直線l：ax+by+c=0，則直線l的方向向量為 =(-b,a)或(b,-a)；

（2）若直線l的斜率為k,則l的一個方向向量為 =(1,k)；

（3）若A(x₁,y₁),B(x₂,y₂),則AB所在直線的一個方向向量為 =(x₂-x₁,y₂-y₁)。

相關定義

有向線段

規定若線段 的端點為起點， 為終點，則線段就具有了從起點 到終點 的方向和長度。

具有方向和長度的線段叫做有向線段。

向量的模

向量的大小，也就是向量的長度(或稱模)。向量 的模記作 。

註：

1．向量的模是非負實數，向量的模是可以比較大小的。向量 ， 。

2．因為方向不能比較大小，所以向量也就不能比較大小。對於向量來說“大於”和“小於”的概念是沒有意義的。例如 是沒有意義的。

單位向量

長度為一個單位（即模為1）的向量，叫做單位向量。與 同向，且長度為單位1的向量，叫做 方向上的單位向量，記作 ， 。

負向量

如果向量AB與向量CD的模相等且方向相反，那么我們把向量AB叫做向量CD的負向量，也稱為相反向量。

零向量

長度為0的向量叫做零向量，記作0。零向量的始點和終點重合，所以零向量沒有確定的方向，或說零向量的方向是任意的。

相等向量

長度相等且方向相同的向量叫做相等向量。向量a與b相等，記作a=b。

規定：所有的零向量都相等。

當用有向線段表示向量時，起點可以任意選取。任意兩個相等的非零向量，都可用同一條有向線段來表示，並且與有向線段的起點無關．同向且等長的有向線段都表示同一向量。

自由向量

始點不固定的向量，它可以任意的平行移動，而且移動後的向量仍然代表原來的向量。

向量

在自由向量的意義下，相等的向量都看作是同一個向量。

數學中只研究自由向量。

滑動向量

沿著直線作用的向量稱為滑動向量。

固定向量

作用於一點的向量稱為固定向量（亦稱膠著向量）。

位置向量

對於坐標平面內的任意一點P，我們把向量OP叫做點P的位置向量，記作：向量P。

相反向量

與a長度相等、方向相反的向量叫做a的相反向量，記作-a，有 -(-a)=a，零向量的相反向量仍是零向量。

平行向量

方向相同或相反的非零向量叫做平行（或共線）向量．向量a、b平行（共線），記作a∥b。零向量長度為零，是起點與終點重合的向量，其方向不確定。我們規定：零向量與任一向量平行。平行於同一直線的一組向量是共線向量。

若a=(x,y)，b=(m,n)，則a//b→a×b=xn-ym=0。

共面向量

平行於同一平面的三個（或多於三個）向量叫做共面向量。

空間中的向量有且只有以下兩種位置關係：(1)共面；(2不共面。

注意：只有三個或三個以上向量才談共面不共面。

法向量

直線l⊥α，取直線l的方向向量a，則向量a叫做平面α的法向量。

法向量

向量的和的模

設平面直角坐標系xOy中，有點A(x₁,y₁)、B(x₂,y₂)，則

。