方向極限

簡介

點（自變數）沿一射線變動時函式的極限稱為方向極限，即在Rⁿ中，自變數x沿某方向趨於a時函式的極限。

在Rⁿ中，當：

n=1時，只有兩種方式：x沿x軸從左方或從右方趨於a，這時得到左、右極限。

當n>1時，有無窮個方向極限：若x沿方向向量為v的直線趨於a，則直線方程為x=a+tv，方向極限可表示為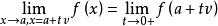

。

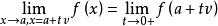
當n=2且a=0時，v=(cosθ,sinθ)，(x,y)→(0,0)的方向極限可表示為

n>1時，從重極限存在可知（在同一點）所有方向極限存在且相等，反之不然。

空間直線的方向用一個與該直線平行的非零向量來表示，該向量稱為這條直線的一個方向向量。直線在空間中的位置，由它經過的空間一點及它的一個方向向量完全確定。

已知定點P₀（x₀,y₀,z₀)及非零向量v={l,m,n}，則經過點Pο且與v平行的直線L就被確定下來，因此，點P₀與v是確定直線L的兩個要素，v稱為L的方向向量。

由於對向量的模長沒有要求，所以每條直線的方向向量都有無數個。直線上任一向量都平行於該直線的方向向量。