基本介紹
- 中文名:n元向量
- 外文名:n-tuple vector
- 別稱:n維向量
- 所屬學科:數學(高等代數)
- 簡介:普通平面和空間向量概念的推廣
基本介紹
n元向量的運算
n元單位向量

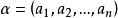

n元向量的相等
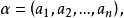
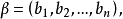

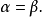
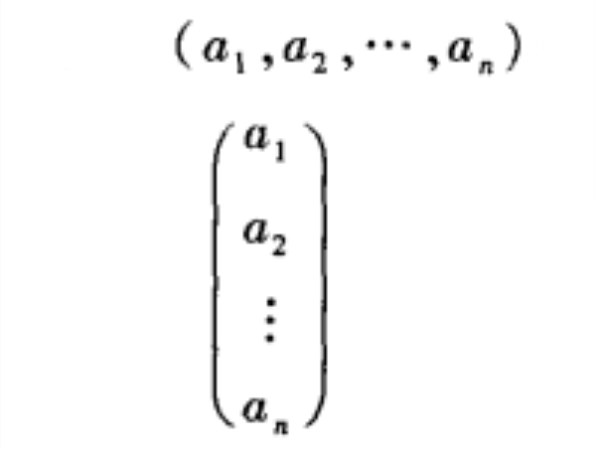

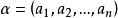

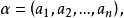
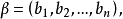

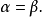
n元向量(n-tuple vector)亦稱n維向量,是通常向量(矢量)的推廣,設P為域,n是正整數,P中n個元素構成的有序組(a1,a2,…,an)稱為P上的n元向量,ai(i=1,2...
,λan)構成域P上的線性空間,稱為域P上n元向量空間。線性空間是在考察了大量的數學對象(如幾何學與物理學中的向量,代數學中的n元向量、矩陣、多項式,分析學中...
線上性代數中,行向量是一個 1×n的矩陣,即矩陣由一個含有n個元素的行所組成即行向量。行向量的轉置是一個列向量,反之亦然。所有的行向量的集合形成一個向量...
在解析幾何中有些事物的性質不能用一個數來刻畫,如一個n元方程組的解是由n個數組成,而這n個數作為方程組的解是一個整體,分開來談是沒有意義的,這時我們就...
線上性代數中,列向量是一個 n×1 的矩陣,即矩陣由一個含有n個元素的列所組成:列向量的轉置是一個行向量,反之亦然。所有的列向量的集合形成一個向量空間,它...
我們知道,一元函式是一個由定義域到值域的映射,其定義域與值域都是一維數集.我們要研究的向量值函式是指分量都是關於同一自變數的一元函式,就是說 n 元向量值...
其中vi是向量在基向量上的投影(即坐標),這裡假設向量空間為n 維。由此,可以直接以坐標向量表示。利用基向量,線性變換也可以用一個簡單的矩陣乘法表示。上述的特徵...
隨機變數可以看作一維隨機向量。稱n元x1,x2,…,xn的函式為X的(聯合)分布函式。又如果(x1,x2)為二維隨機向量,則稱x1+ix2(i2=-1)為復隨機變數。 隨機...
向量自回歸模型VAR模型的公式 編輯 VAR模型描述在同一樣本期間內的n個變數(內生變數)可以作為它們過去值的線性函式。 一個VAR(p)模型可以寫成為:Yt=c+A1(yt-...
由於中斷向量表中的向量是按中斷號順序排列,因此給定一個中斷號N,那么它對應的中斷向量在記憶體中的位置就是0x0000:N×4,即對應的中斷服務程式入口地址保存在物理...
再如,域P上所有n元向量(a1,a2,…,an)構成的集合P對於加法:(a1,a2,…,an)+(b1,b2,…,bn)=(a1+b1,a2+b2,…,an+bn)與純量乘法:λ(a1,a2,…,an...
n維歐幾里得空間(n-dimensional Euclidean space)是現實空間的抽象與推廣,簡稱n維歐氏空間。n維歐氏空間在代數中是定義了內積的n維線性空間,記為Rn,其元素是n維向量,...
除非負條件外的n個約束條件所組成的n元方程組,若可解可求出n個變數xj的值。求出的n個變數所構成的列向量X=(x1,···xn)T,若能再滿足非負條件(即決策...
logspace是一個MATLAB類型的函式,相關函式是linspace。其功能是行向量,生成從10的a次方到10的b次方之間按對數等分的n個元素的行向量。n如果省略,則默認值為50。在...
多元多項式(polynomial of several variables )是一元多項式的推廣,它是多項式理論研究的重要對象。有限多個單項式之和(假設其中不含同類項)稱為n元多項式,簡稱多項式...
n階矩陣A相似於對角矩陣的充要條件是A有n個線性無關的特徵向量。 [3] 證明過程:(1)必要性。設有可逆矩陣P,使得令矩陣P的n個列向量為 ,則有...
這就是為什麼只稱二維向量的為複數,而不稱其他向量為複數的道理。當n>2時,n維向量空間不再稱為數域而稱為超複數系統。四元數域運算 編輯 ...
多元分析發展的初期,主要討論如何把一元正態總體的統計理論和方法推廣到多元正態...設已知N個觀測值X1,X2,…,Xn,每個觀測值是一個p維向量(如上例中人的身高...
