單值化定理

單值化定理(uniformization theorem)是黎曼曲面理論中最基本最重要的定理。單值化定理表明，大多數的情形下，黎曼曲面共形等價於單位圓D對某個富克斯群G的商空間D/G，因此R上的解析函式論等價於定義在D上的對某個富克斯群G自守的函式論，反之，整個黎曼曲面理論也能以這個特殊的表示為基礎進行討論，一個經典的問題是：給定一個D上的富克斯群G，是否存在非常數亞純函式對於G是自守的，即黎曼曲面上是否存在非常數的亞純函式。龐加萊((J.-)H.Poincaré)具體構造Θ級數，後稱為龐加萊級數，以此證明對給定的G是自守的函式的存在，閉黎曼曲面的一個重要定理是黎曼-羅赫定理，它給出閉黎曼曲面上亞純函式構成的線性空間的維數，兩黎曼曲面，如果存在映一個為另一個的共形映射，則稱它們是共形等價的。關於閉黎曼曲面的模的黎曼問題稱：虧格為g(>2)的閉黎曼曲面的共形等價類集合R_g構成3g-3維複流形，這方面基礎性的工作是由弗里克(R.Fricke)和泰希米勒(O.Teichmǚller)所做。

基本介紹

• 中文名：單值化定理
• 外文名：uniformization theorem
• 所屬學科：數學
• 所屬問題：複變函數論(黎曼曲面)
• 相關概念：黎曼曲面，覆蓋空間等

基本介紹

單值化定理敘述如下：

任一黎曼曲面必共形等價於下述典型曲面之一：

1.擴充複平面 ；

2.複平面C；

3.穿洞的複平面 ；

4.環面，即 ，Z表示整數集；

5.單位圓對某個富克斯群G的商空間D/G。

相關介紹

覆蓋空間

設X和Y是Riemann曲面，一個映射 稱為覆蓋映射，若對每點 ，有開鄰域 使得

其中 是Y的互不相交的開子集，且 在 上的限制 是同胚的。顯然覆蓋映射是局部同胚的，Y稱為X的一個覆蓋空間，如果存在覆蓋映射 ，使得 。

每個覆蓋映射 都具有曲線提升性質：即對每條曲線 及每個點 使得 ，或者說對每個 ，存在一條曲線 使得 且 ，見交換圖(圖1)。 就稱為以 為起點的 在Y上的提升。

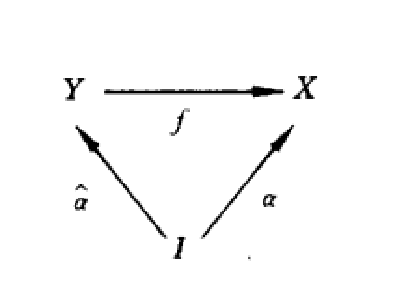圖1

設Y是X的覆蓋空間 是覆蓋映射，若Y是單連通的，則稱Y為X的萬有覆蓋空間，由如下結論，我們可以進一步認識萬有覆蓋空間，Y為X的萬有覆蓋空間若且唯若相應的覆蓋映射具有萬有性質：對每個覆蓋映射 ，其中Z為Riemann曲面以及對每對 使得 ，存在惟一連續映射 使得 且有交換圖如2，即, 。使交換圖成立的h又稱為保網的，這是很形象的。

設 是萬有覆蓋映射，則對每對 使得 ，由萬有性質，即對交換圖2中 的情形，存在惟一的保網同胚 使得 ，此時h稱之為覆蓋變換，所有這樣由 確定的保網同胚映射，即覆蓋變換之集在複合運算定義的乘法下構成一個群，稱之為覆蓋變換群，記為 ，它同構於X的基本群。

圖2

設 ，對任一點 ，令

稱為(y所在的)軌道。我們把 視為一點，這樣的點構成的集記為 ，並可以賦上開集系統和復結構使其成為一個Riemann曲面，開集系統和復結構都是由投影映射 導出來的，要求使得是Y到的萬有覆蓋映射，且是解析的，進而X與是共形等價的，即X與間存在雙方解析同胚。在共形等價意RT，可寫。故X是它的萬有覆蓋空間在覆蓋變換群下的粘合空間——商空間。

設 為萬有覆蓋空間。若X是單連通的，那么 是平凡的。由於與同構，所以它也是平凡的，即它只包含一個恆等覆蓋變換。這樣是單葉的，從而是Y到X的同胚。進一步，是雙方解析的，即Y與X是共形等價的。這說明了同一個Riemann曲面的兩個萬有覆蓋空間是共形等價的，因為它們互為萬有覆蓋空間。

對任一Riemann曲面X，我們以X上曲線的同倫等價類作為特徵將X的點區分為各個層葉，這樣做可使得曲面X上的每個“洞”被“捏”起來，從而建立X上的一個單連通的覆蓋Riemann曲面——萬有覆蓋空間。為此，取一點a∈X，對任意，讓表示分別以a和x為起點和終點的X上的曲線的同倫等價類之集，定義

以及映射使得。然後，在上建立開集系統和復結構，使成為一個單連通的Riemann曲面，並且使得是萬有覆蓋映射，所以任一Riemann曲面都有萬有覆蓋空間。

單值化定理

單連通的Riemann曲面共形等價於Riemann球面或複平面或單位圓盤△。因此任一Riemann曲面X以球面或複平面或單位圓盤△為其萬有覆蓋空間。這樣，Riemann曲面X被分為橢球面或拋物面或雙曲面，根據它的萬有覆蓋空間為球面或複平面或單位圓盤△來確定，進一步研究得到穿孔平面和環面T是拋物的，即它們的萬有覆蓋空間為複平面就是萬有覆蓋映射，因是單連通的，並且

exp把上的平行於虛軸寬為的帶形格子的兩邊粘合起來，得到兩頭無限延伸出去的管子。這個管子共形等價於；因環面可寫為，其中是格子，那么投影映射，就是萬有覆蓋映射，並且

所有不與共形等價的Riemann曲面一定是雙曲的，對任意雙曲Riemann曲面中的每個覆蓋變換是△到△的共形映照，從而是線性變換，即是△上變換群的子群，可以寫。