龐加萊複數平面模型(Poincaré complex plane model)是解釋羅氏平面幾何的模型。這個模型是龐加萊((J.-)H.Poincaré)首先提出來的,因為該模型的點是在複數上半平面上,所以稱之為羅氏幾何的龐加萊複數平面模型。龐加萊利用這個模型,在歐氏平面上解釋了羅氏平面幾何,若歐氏幾何無矛盾,則羅氏幾何亦無矛盾。
基本介紹
- 中文名:龐加萊複數平面模型
- 外文名:Poincaré complex plane model
- 所屬學科:數學
- 所屬問題:高等幾何(非歐幾里得幾何)
- 提出者:龐加萊((J.-)H.Poincaré)
基本介紹,龐加萊簡介,
基本介紹
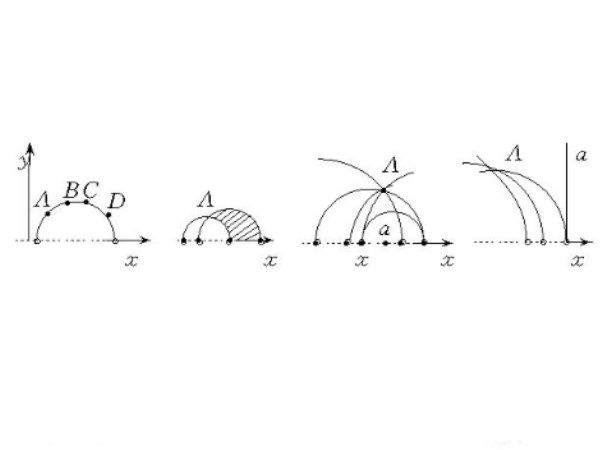
龐加萊複數平面模型是解釋羅氏平面幾何的模型。取歐氏上半平面,其中的點稱為羅氏點(不包括x軸上的點),羅氏直線是指中心在x軸上不含有端點的半圓周以及上半平面中垂直於x軸的半直線(不含有x軸上的點,這樣的半直線可以看成中心在x軸,半徑為無限大的半圓周),它們統稱為歐氏半圓周或羅氏直線,端點為A,B的半圓弧表示羅氏線段AB.用起點在上半平面,終點在x軸上的弧OX表示羅氏半直線(X不是羅氏點),羅氏角是指通過一點的兩條羅氏半直線的集合。
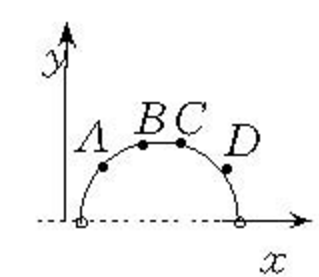 圖1
圖1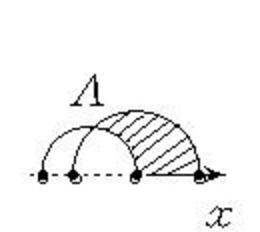 圖2
圖2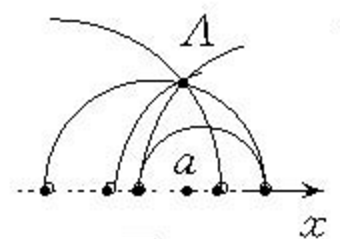 圖3
圖3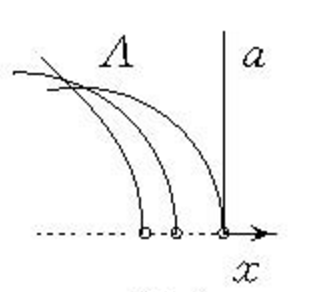 圖4
圖4對應於歐氏點和半圓周,在羅氏點和羅氏直線之間建立如下的關係:
1.若點A在半圓周a上,則稱羅氏點A在羅氏直線a上。
2.設A,B,C在半圓周a上,若B在A與C之間,則稱羅氏直線a上的點B在A與C之間,即點在羅氏直線上的順序與點在歐氏半圓周上的順序相同。
3.這樣的羅氏直線上存在戴德金原理。
4.在上半平面引進複數,使每一點M與一個複數x+iy之間建立對應,這樣可以利用對半圓周的反演變換定義契約關係,即若經過幾個反演變換的乘積把一個圓弧(角)變成另一個圓弧(角),則稱這兩個羅氏線段(羅氏角)是契約的。
利用這些關係就可以證明這個模型滿足羅氏平面幾何的全部公理。例如,它滿足羅氏幾何的平行公理,若a是羅氏直線,A∉ a,過A可以引無數多條羅氏直線,與a沒有公共點。即通過羅氏直線外的任意一點,可以引無數多條羅氏直線,與已知的直線共面而不相交。
龐加萊簡介
龐加萊,法國人。1854年4月29日生於南錫市。他對數學深感興趣,於1876年寫出了論文《關於微分方程所定義的函式的性質》,於1878年發表在《高等工藝學校學報》上。同年,他寫出了博士論文《自變數為任意個數的偏微分方程的積分》,獲得了巴黎大學數學博士學位。1879年起龐加萊任卡恩大學教授。1881年起執教於巴黎大學。1908年被選為法國科學院院士。1912年7月17日在巴黎逝世。
 龐加萊
龐加萊龐加萊是19世紀末20世紀初國家數學界的領袖人物,是一位對數學及其套用做了廣泛的獨創性、奠基性工作的大師。
首先,他創立了自守函式理論和微分方程定性理論。自守函式就是在某些變換群作用下不變的函式,它是圓函式、雙曲函式、橢圓函式的推廣。龐加萊深入研究了常微分方程所定義的積分曲線的形狀和奇點的性質。他創立了研究微分方程的新方法,即不求解方程,而從方程本身出發,直接研究積分曲線的性質,就是解的性質。這個方法被稱為微分方程的定性理論。
其次,龐加萊是組合拓撲學的奠基人。他研究了代數函式f(x,y,z)=0當x,y,z都是複數時的四維曲面的結構。值得一提的是,1912年他在逝世前不久得到了一個有重要價值的不動點理論:如果平切環的一個自身到自身的拓撲變換把它的一邊(是圓周)沿著一個方向轉動,而把另一邊沿著相反的方向轉動,同時保持面積不變,則在平切環里至少存在兩個不動點。
第三,龐加萊在非歐幾何、代數幾何、偏微分方程、積分方程等領域裡也作了許多貢獻。如獨立地得到了平面雙曲幾何的龐加萊模型;在代數幾何中得到了一個普遍的單值化定理,並於1907年完成了這個定理的證明;1894年證明了偏微分方程 (這裡
(這裡 是複數,在區域邊界上u=0)在一個有界三維區域內的所有特徵值的存在性及基本性質;等等。
是複數,在區域邊界上u=0)在一個有界三維區域內的所有特徵值的存在性及基本性質;等等。


龐加萊也是一位物理學家。
龐加菜同時還是一位自然科學哲學家,他主張數學的對象及真理不能脫離數學的真理或直覺而獨立存在,它們應當能夠通過理性的活動或直覺的活動而獨立存在。發表了一系列的自然哲學名著。