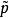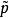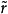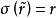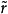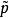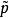萬有覆蓋曲面

覆蓋曲面是黎曼曲面理論中引進的重要概念。萬有覆蓋曲面是常見的三種覆蓋曲面之一。

基本介紹

• 中文名：萬有覆蓋曲面
• 外文名：universal covering surface
• 適用範圍：數理科學

簡介

跡群

投影映射作為連續映射誘導的基本群與 R 的基本群 F 的子群 G 同構，並稱 G 為的跡群，記。反之，對 R 的基本群 F 的任意子群 G ，恆存在一個非限覆蓋曲面，使得其基本群的跡群為 G 。

萬有覆蓋曲面

若 G 只包含 F 的么元素 e ，則相應的覆蓋曲面稱為萬有覆蓋曲面，它是單連通的覆蓋曲面。

非限覆蓋曲面

σ 為投影映射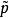，是 p 上的點， p 為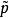的投影。設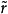和 r 分別是和 R 上的曲線，若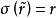，則稱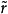是 r 的提升。若對任意的 R 上的曲線 r 和 r 的起始點上的任意點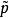，r 的以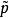為起始點的提升總存在，則稱為 R 的非限覆蓋曲面。

黎曼曲面

在數學中，黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而提出的一種曲面。用現代的語言說，黎曼曲面就是連通的一維複流形。

黎曼曲面的研究不僅是單複變函數論的基本問題之一，而且與眾多的現代數學分支有緊密聯繫，如多複變函數論、複流形、代數幾何、代數數論、 自守函式等。