覆蓋曲面是黎曼曲面理論中引進的重要概念。常見的覆蓋曲面有:非限覆蓋曲面、光滑覆蓋曲面、萬有覆蓋曲面三種。
基本介紹
- 中文名:覆蓋曲面
- 外文名:covering surface
- 適用範圍:數理科學
概念
相關類型
非限覆蓋曲面


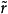


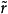




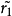

光滑覆蓋曲面



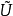


萬有覆蓋曲面


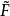
覆蓋曲面是黎曼曲面理論中引進的重要概念。常見的覆蓋曲面有:非限覆蓋曲面、光滑覆蓋曲面、萬有覆蓋曲面三種。


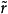


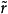




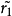




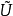
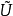



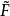
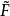

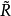
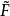
覆蓋曲面是黎曼曲面理論中引進的重要概念。常見的覆蓋曲面有:非限覆蓋曲面、光滑覆蓋曲面、萬有覆蓋曲面三種。...
覆蓋曲面是黎曼曲面理論中引進的重要概念。萬有覆蓋曲面是常見的三種覆蓋曲面之一。...
在數學中,黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而提出的一種曲面。用現代的語言說,黎曼曲面就是連通的一維複流形。黎曼曲面的研究...
《黎曼曲面》主要介紹Riemann曲面的基本理論,包括:Riemann曲面的概會、weierstrass意義下的解析函式與Riemann曲面、覆蓋曲面、微分形式與微分、單值化定理及其套用、微分...
只有一個側面的曲面(通常的曲面都有兩個側面),即不可定向的曲面,稱之為單側曲面(one-sided)。單側曲面並不多,一個著名的單側曲面是:莫比烏斯帶(Mobius Strip...
Riemann曲面是一個連通的一維復解析流形,從某種意義上講可以看成是複平面上區域的推廣。顯然Riemann曲面是一維複流形,因此一個Riemann曲面總是可以定向的。若Riemann...
汽車覆蓋件是指覆蓋發動機、底盤,構成駕駛室、車身的金屬薄板製成的空間形狀的表面或內部零件。按功能和部位可分為外部覆蓋件、內部覆蓋件和骨架覆蓋件三類。它們在...
《完備開曲面上全曲率的幾何》系統地介紹了2維完備非緊緻黎曼流形上全曲率的幾何,其中包括黎曼幾何預備知識,Cohn Vossen定理,Huber定理,理想邊界,割跡的結構,等周...
覆蓋曲面是黎曼曲面理論中引進的重要概念。光滑覆蓋曲面是常見的三種覆蓋曲面之一。...
覆蓋曲面是黎曼曲面理論中引進的重要概念。非限覆蓋曲面是常見的三種覆蓋曲面之一。...
薄殼結構是建築學上的術語。殼,是一種曲面構件,主要承受各種作用產生的中面內的力。薄殼結構就是曲面的薄壁結構,按曲面生成的形式分為筒殼、圓頂薄殼、雙曲扁殼...
單值化定理(uniformization theorem)是黎曼曲面理論中最基本最重要的定理。單值化定理表明,大多數的情形下,黎曼曲面共形等價於單位圓D對某個富克斯群G的商空間D/G...
描述曲面尺寸準確度的主要指標為輪廓度誤差,它是指被測實際輪廓相對於理想輪廓的變動情況。...
Rhino適應於機械設計,進行簡單的曲率分析,但無法調整曲面光滑度;CATIA適應於3D建築設計、分析、裝配,且覆蓋了所有類型的設計和工程需求,如曲率分析、曲面光滑度的自動...
在一般情況下,磁通量是通過磁場在曲面面積上的積分定義的。其中,Φ為磁通量,B為磁感應強度,S為曲面,B·dS為點積,dS為無窮小矢量(見曲面積分)。磁通量通常通過...
在幾何學中,偽球面用於描述具有恆定負高斯曲率的各種表面。 根據套用環境,它可以指恆定負曲率的理論表面,如牽引曲線或雙曲面。偽球面是由曳物線(tractrix)繞其...
