偽球面

簡介

在幾何學中，偽球面用於描述具有恆定負高斯曲率的各種表面。根據套用環境，它可以指恆定負曲率的理論表面，如牽引曲線或雙曲面。

偽球面是由曳物線(tractrix)繞其漸近線旋轉而形成的迴轉曲面。這種曲面的全曲率在每一點都是常數且是負的。位於此曲面上的直線與平行公設不一致，因而構造這種曲面的可能性為非歐幾何學提供了相對相容性的證明。

一般認為，半徑為R的偽球體的曲率均為

，這類似於半徑為R的球體，其曲率為

類似。該術語由Eugenio Beltrami在1868年發表的有關雙曲線幾何模型的論文中有所介紹。

該術語也用於指某特定表面的一種，即Tractricoid表面：一種關於其漸近線旋轉的結果。例如（半）假球（半徑為1）是輪廓被參數化的表面，

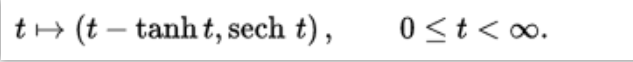
它是一個奇異的空間（赤道是一個奇點），但是遠離奇異點，它具有恆定的負高斯曲率，因此在雙曲面上是局部等長的。

之所以叫做為球面是因為它是一個恆定的負曲率的二維表面，就像具有正高斯曲率的球體一樣。正如球體在每一點上都是圓頂的正彎曲幾何形狀一樣，整個假球體在每一點都具有鞍座的負彎曲幾何形狀。

早在1693年，Christiaan惠更斯發現，儘管沿著旋轉軸線的形狀是無限大的程度，假球的體積和表面積是有限的。對於給定的邊緣半徑R，面積為4π

，就像球體一樣，而體積是

，因此是該半徑球體的一半。

彎曲半空間由y≥1的雙曲上半平面的部分覆蓋。覆蓋圖在周期2π的x方向上是周期性的，並且對於產生偽球的軌道，將偽圈的經線和垂直測地線x = c的環繞y = c。該映射是局部等值線，因此表現出上半平面的y≥1作為偽球的通用覆蓋空間。精確的映射是，

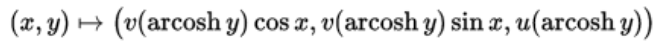
此時，

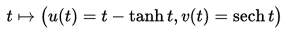
是上面的系統的參數化。

在使用雙曲面模型的一些來源中，雙曲面被稱為偽球。這個詞的使用是因為雙曲面可以被認為是虛擬半徑的球體，嵌入在閔可夫斯基空間中。