只有一個側面的曲面(通常的曲面都有兩個側面),即不可定向的曲面，稱之為單側曲面（one-sided）。單側曲面並不多，一個著名的單側曲面是：莫比烏斯帶（Mobius Strip)，也叫莫比烏斯圈，另外還有克萊因瓶等。
基本介紹
- 中文名：單側曲面
- 外文名：one-sided surface
- 定義：只有一個側面的不可定向的曲面
- 舉例：莫比烏斯帶、克萊因瓶等
- 相關概念：光滑曲面、法線、雙側曲面等
基本介紹,詳細介紹,
基本介紹
在光滑曲面
上任取一點
，過點 的法線有兩個方向，如果選定法線的某個方向為指定的方向，當點在曲面上連續移動時，法線也連續變動、當動點從 出發沿著曲面上任意一條不越過曲面邊界的封閉曲線又回到原位置 時，法線的指向保持不變，稱這種曲面為雙側曲面，否則稱其為單側曲面。
單側曲面是存在的，所謂的莫比烏斯帶(Mobius帶)就是這類曲面的一個典型例子，如果把一長方形紙條ABCD先扭一次，再粘起來，使A點與C點相合，B點D點相合，這樣就可得到它的一個模型。假若用顏色來塗它，那就可以不跨它的邊緣而用這種顏色塗遍該帶的全部。
詳細介紹
許多多面體和閉曲面的連通度都是奇數。於是自然會發生這樣的問題：有沒有連通度為偶數的閉曲面呢?換句話說，有沒有按拓撲性質來說，介於球面和環面之間或者介於兩個“圈餅”之間的曲面呢?
答案是肯定的。可作出一個多面體——七面體，其連通度按多面體的歐拉定理等於2，這些目的，我們從有8個三角形面的正八面體開始(圖1)，增添由對角線決定的三個正方形面(例如圖1的ABCD)。用這種方法得出含十一個面的圖形，它不符合多面體的定義，因為交於每個棱的面數是三個而不是兩個，現在我們去掉四個三角形：從圖形的前部(按照圖1的位置)去掉左上角的三角形和右下角的三角形，從圖形的後部去掉左下角的三角形和右上角的三角形，這樣一來，只剩下了有陰影線的四個三角形，總共我們得出由四個三角形和三個正方形組成的圖形，這圖形的棱和頂點是八面體的棱和頂點，但八面體的對角線卻不是我們的圖形的棱而是面的自交線，顯然在每一棱上恰有二面相遇，而且我們可從任一面開始走起，越過若干個棱而達到任一別的面，所以這圖形是多面體，由於它有七個面，所以叫做七面體，跟八面體一樣，七面體也有十二個棱和六個頂點，由推廣的歐拉多面體公式得方程
圖1由此得出七面體的連通度h=2，正像簡單多面體經過連續變形最後能變成球面一樣，七面體經過連續變形也能變成一個簡單而閉合的曲面，這種曲面稱為“羅馬式曲面”，是斯坦納(Steiner)研究過的，像七面體一樣，這種曲面自交於三條相互垂直的線段，它的方程以直角坐標表示時是
七面體除了有偶數連通度和自交線外，還有此前我們未討論過的另一重要性質，構想七面體是用薄膜作的，有一個會爬的小動物，例如甲蟲，從曲面上的一點P開始爬行，在薄膜的另一側正對著點P有另一點P’——如果薄膜換成原來的幾何曲面，那么P’就和P重合了。可能有人會這樣想，甲蟲若不在薄膜的某處咬破一個洞就不能從點P爬到點P’，對於球面和一切“圈餅”來說，情形確實是這樣的，可是對於七面體來說就不對了。在平行於圖2的平面的正方形面朝著觀察者的一側上選擇一點P，作為甲蟲的出發點(圖2)。考慮七面體上從點P出發越過1，2，3，4諸棱又回到原來正方形面的一條道路，顯然甲蟲從正方形面向前的一側開始，順著這條道路爬行，越過標號4的棱到達原正方形面的背後，甲蟲當然要在三個地方穿過薄膜，但每次被鑽穿的面乃是在七面體自交線上阻礙交通的那個面，而不是甲蟲在其上爬行的面。
圖2由於這種理由，七面體稱為單側曲面，而球面和前面講過的各種“圈餅”稱為雙側曲面，此種分類法也適用於有邊緣曲面，構想有邊緣曲面也是由薄膜製成的，試決定在薄膜上有沒有從一側出發到另一側的通路，中途不許越過邊緣，也不許穿過薄膜。如有這種通路存在，則曲面稱為單側的，否則稱為雙側的。圓面等邊緣曲面，都是雙側的，但是也可以舉出一個比七面體更簡單的有邊緣的單側曲面的例子，這就是莫比烏斯帶，莫氏帶可用一張細長的長方形紙條作成，如圖3所示，把兩邊AB和CD粘起來，使A和C重合，B和D重合，則得到一圓筒形帶，如前所述，這是雙側有邊緣曲面，另一方面，若在兩端黏合之前，把一端相對於另一端扭轉180°，然後再使A，D重合，B，D重合，便得到莫比烏斯帶的模型(圖4)。容易看出，這種曲面是單側的，因為，在兩端黏合之前作一條直線，比方說是PP’，平行於帶子的長邊，則在兩端黏合之後，直線PP’就變為從帶子一側到另一側的通路QQ’。
圖3
圖4單側曲面也可以用另一種重要的拓撲概念來刻畫，而不必假借曲面是由薄膜製成的，構想任一給定曲面上的每一點(邊緣上的點除外，如果有的話)被安全在這曲面上的一條小閉曲線所包圍，現在對所有的這些曲線如此規定指向，使充分靠近的二曲線的指向相同，如果規定這樣一種行進的指向是可能的，則稱這樣的一個規定為曲面的一個定向，而曲面稱為可定向的。現在我們證明，單側曲面不可定向。為了證明，我們考慮和曲面的單側性等價的一條閉路。比如說，在莫比烏斯帶上選好一條道路QQ’，其中的Q和Q’兩點還是當做疊合的，讓我們給Q指定一個指向，指向既經確定，在整個道路QQ’上就一直沿用它，這樣，當動點又來到Q’=Q時，則伴隨Q’的指向必同Q的相反，假如莫比烏斯帶是可定向的，這種現象便不會發生，所有別種形式的單側曲面也和莫氏帶有類似的情況，反轉來也可以證明，所有雙側曲面都是可定向的，由此可知，曲面的雙側與單側之分，和曲面的可定向與不可定向是一回事。
容易懂得，曲面之不可定向，等價於曲面上存在一條閉曲線s，當圓心在這條曲線上連續運動時，有指向的小圓帶著相反的指向回到出發點(例如圖4中的曲線QQ’)。在這樣的曲面上，沿著曲線s的一側行進，雖然沒有越過曲線，也將達到它的另一側，由於這種原因，s稱為單岸曲線，雖則一個可定向的曲面上所有的曲線都是雙岸的，但單岸閉曲線的存在卻是不可定向曲面的特徵，曲面的單側性同曲面上存在單岸曲線是等價的。前一性質涉及曲面在空間中的位置，後一性質涉及曲線在曲面上的位置。
七面體有自交線，這一點跟莫比烏斯帶不同，那么試問任何單側閉曲面是不是都自交呢?假如曲面只有一側，就不可能把空間的一部分同其餘的部分分開，即不能把空間分為“內”“外”兩部，不自交的閉曲面是不可想像的，事實上，所有單側閉曲面都要自交，不過這句話的證明，必須另謀途徑。
並不是說無論什麼曲面的自交都是拓撲性質。例如，考慮圖5所畫的曲線繞虛線為軸旋轉而得的曲面，這一曲面有自交線，即點A所作的圓，但曲面經連續變形，可變成如圖6中的曲線所產生的迴轉曲畫，當然這個曲面沒有自交線，因此同球面等價。反過來球面也可以經過變形而變為第一個迴轉曲面，由此可見，自交線的存在不一定就表示拓撲性質。在這個例子裡，自交線作成一閉曲線，另一方面，七面體的自交線有六個端點，即七面體的六個頂點，這些點其實應該當做奇點看待，因為曲面上任何正則點的鄰域總可經過變形而成為圓面，但對七面體頂點的鄰域則不可能這樣作(參考圖1)，所以七面體有六個奇點，從這裡又引出一個問題：有沒有無奇點的單側閉曲面呢?
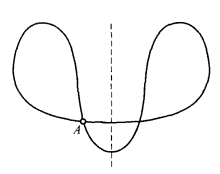圖5
圖6有的，這樣的曲面第一次被克萊因發現，我們從一個兩頭開口的管子出發(圖7)，從這種管子可得到環面：把管子彎曲，一直彎曲到兩端相遇，然後將兩圓口粘在一起。
圖7現在我們改用另一種方法將兩端黏合，先將管子的一端捏得比另一端稍細一些，將細的一端掉過頭來插入粗的一端的管壁內，使二瓶口作同心圓狀(圖8)．隨後將小口放大，大口縮小，使兩口重合在一起，最後把它們粘起來，這樣得到的曲面沒有任何奇點；它叫做克萊因曲面(也叫做“克萊因瓶”)，其形狀如圖9．這種曲面顯然是單側的，並且在細端插入管壁處沿一閉曲線自交。
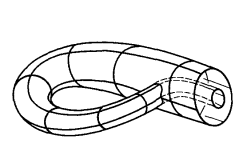圖8
圖9第一個單側閉曲面的例子——七面體，跟前面討論過的各種雙側閉曲面不同的地方，在於七面體有偶數的連通度．那么我們可不可以抱著同樣的希望，說克萊因瓶的連通度也是偶數的呢?不可以，事實上克萊因瓶的連通度跟環面一樣，是3。為了證明，我們也可以像對待環面那樣，來選擇克萊因瓶的典型截口組，可以選擇瓶子兩端的接縫作為組中的第一條閉曲線，沿著這條曲線剪開，把曲面拉直使成為圓筒形，然後選擇圓筒上的一條母線作為組中的第二條曲線，沿著這條母線將曲面剪開，於是克萊因瓶就變為矩形，像環面一樣，再過矩形邊緣上任意兩點作曲線，曲面就被分成兩片了，套用連通度的一般定義於克萊因瓶，可知
，故
，這正是我們要證明的。
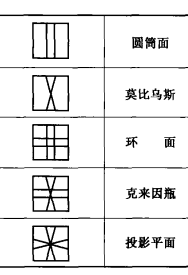表1 五種曲面及其相應特徵
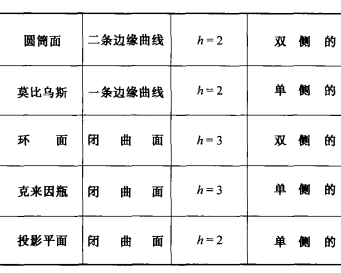表二 五種曲面及其相應特徵現在，我們已能以不同的方式疊合矩形(或正方形)的對邊，得出五種不同的曲面莫比烏斯帶的模型可以從克萊因曲面消去一組對邊的疊合關係而得出，因此一定能夠把克萊因瓶沿著一條適當選擇的閉曲線剪開，使成為莫比烏斯帶，圖10、11表示用另一種方法把克萊因瓶剪成二條莫氏帶，建議讀者作出正方形模型的對應演變過程。
圖10
圖11在我們討論過的一些單側閉曲面里有連通度為偶數的(例如七面體)，也有連通度為奇數的(例如克萊因瓶)；另一方面，我們講過的一切雙側閉曲面的連通度都是奇數，進一步可以證明，並無連通度為偶數的雙側曲面。
正像正方形一樣，一切其他的正4p邊多邊形也可以用不同的疊合方式由它得出許許多多的曲面模型，其中包括有邊緣和無邊緣的，單側和雙側的，如果在圖12上的AB和CD是4p邊形中將要疊合的二邊，則有兩種可能的疊合方式：(1)連結對應點的二直線不相變；(2)這樣的二直線相交，例如在圖12上，第一種情形由疊合A，C而得，第二種情形由疊合B，D而得。現在我們斷言：如果4p邊形的任意二邊是按照第二種方式對應的，則無論其他的邊如何對應，所得的曲面永遠是單側的。
圖12為了證明這句話，即證明多邊形所代表的曲面不可定向，設P和P’是在疊合中AB和CD上的二對應點(圖12)，那么直線PP’代表曲面上的一條閉路，用R代表在曲面上沿這條路線運動的一點，R先經過P，又由P’回到原處，讓我們給曲面上點兄指定一個繞行指向，這個指向在R行進時沒有任何不連續的變化，為此我們以R為圓心作一小圓，並以箭頭表示它的指向，把小圓隨著R連續移動，只要整個圓在4p邊形內，它就是多邊形代表的曲面上一閉曲線的象，當R接近P時，只有圓弧ST仍留在4p邊形內，要想得到曲面上閉曲線的象，必須利用在直線CD上和S，T對應的點S’，T'．但因為AB和CD的疊合是第二類的，S和S’在直線PP'的不同側，T和T'也如此。這樣一來，在曲面上帶有繞行指向的閉曲線由二有向弧
和
代表，當R達到P然後從P’回到原來位置時這條曲線沒有不連續的變化，隨著動點R與P’的距離逐漸增加，弧ST逐漸消失，而弧S'T'變為整個圓．但是這圓的指向同原來圓的相反，這就證明了曲面是不可定向的。
作為這個定理的特例，我們得到投影平面是單側的結論。因為，在投影平面模型里，所有的對應關係都是第二類的。
反轉來容易證明，如果所有的對應關係是第一類的，則模型永遠代表雙側曲面。
我們已經從球的表面得出投影平面模型，另一方面，我們見過克萊因瓶同環面也有關係，雖然這種關係不同於球面和投影平面的關係，我們現在指出，事實上也可以在克萊因瓶和環面之間建立像球面與投影平面之間一樣的對應關係，一般地，對任何單側曲面，必有一雙側曲面同它對應。
要想從球面得到投影平面，必須把球面的對徑點疊合起來，現在我們把類似的做法套用於環面，從環面任一母圓和圓心作環面的軸的垂線，這二直線的交點M叫做環面的中心(圖13)，設P是環面上的任一點，則P對於點M的對稱點P'也必在環面上，環面上每對對於點M對稱的點叫做對徑點，把每對對徑點看做一點，球面就變成一新的曲面F，今證明F便是克萊因瓶。
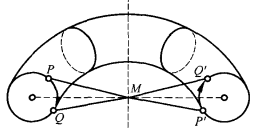圖13試考慮環面上的一母圓，這母圓對應第二個母圓，如圖13所示，二母圓把環面分成兩半，曲面F是由去掉環面的一半，並把剩下的一半的邊緣圓周上的點如圖上指出的方式疊合而成的，相仿地，我們曾經用半球面代替球面來構成投影平面，考慮到二疊合圓的繞行指向，可知半環面由疊合而變成克萊因瓶。
顯然第二個半環面可以覆蓋在第一個半環面上，使原來的每對對徑點現在都重合，但是，這裡必須把第二個半環面的裡面翻到外面來，像翻手套一樣，如果再把這兩個半球面粘起來，最後就得雙重覆蓋的克萊因瓶，由於這種理由，環面可叫做克萊因瓶的雙葉覆蓋曲面。同理，球面叫做投影平面的雙葉覆蓋曲面，一般地可以證明，每一單側曲面有一雙側曲面作為它的雙葉覆蓋曲面。
