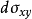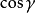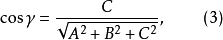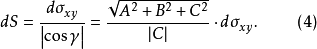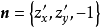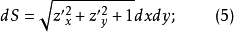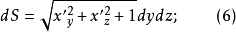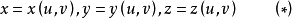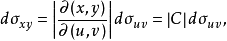給定曲面xi=fi(u,v)(i=1,2,3)，如果函式fi(u,v)是連續可微的，並且雅可比行列式∂(f1,f2)/∂(u,v)，∂(f2,f3)/∂(u,v)，∂(f3,f1)/∂(u,v)不同時為0，則這一曲面稱為光滑曲面(smooth surface)。如果fi(u,v)是k次連續可微的，則這一曲面稱為Ck類曲面。如果fi(u, v)是解析函式，則這一曲面稱為解析曲面。.從幾何直觀上看，所謂曲面是光滑的，是指曲面在每點都有切平面，並且切平面的方向隨著曲面上點的連續變動而連續變化，說曲面是分片光滑的，是指曲面是由有限個光滑曲面並起來的。比如球面是光滑曲面，長方體的邊界面則是分片光滑曲面。
基本介紹
- 中文名：光滑曲面
- 外文名：smooth surface
- 所屬學科：數學（高等數學）
- 簡介：有連續變動的切平面的曲面
基本介紹,光滑曲面的面積,
基本介紹
光滑曲面是指有連續變動的切平面的曲面，或者說有可以處處連續移動的單位法向量的曲面.若D是R2中有界的若爾當可測閉區域，向量值函式φ：D→R3是C1類的(這意味著φ在包含D的某個開集上是C1類的)，且對任意t∈D，D1φ(t)×D2φ(t)≠0(即雅可比矩陣Jφ(t)的秩是2)，這裡D1，D2表示偏導數，則點集S=φ(D)稱為R3中的光滑曲面。又若φ對D的內部的限制是單射，則S稱為簡單光滑曲面。當f連續可微時，凡是可以用形如z=f(x，y)表示的曲面S，都是簡單光滑曲面。由於上述定義中涉及曲面的參數表示φ，因此可以發生這樣的情況：一種表示滿足定義，另一種表示不滿足定義.但只要有一種表示滿足定義，就說曲面是光滑的.在光滑曲面上，單位法向量函式(D1φ×D2φ)/|D1φ×D2φ|是連續的。設φ：D→R3與ψ：E→R3是曲面S的兩個參數表示，若存在C1類雙射g：E→D，使ψ=φ°g，則稱φ與ψ是光滑等價的。若g還滿足Jg>0，則稱g保持定向，並稱φ與ψ定向等價;若Jg<0，則稱g反轉定向，這裡Jg是g的雅可比行列式.延伸至無限遠的曲面，若任何有界的部分是光滑的，則曲面稱為光滑的。
光滑曲面的面積
設S是一塊空間光滑曲面——即具有連續變動的切平面的曲面。S在xy面上的投影是Dxy,dS是S上一小曲面塊(同時表示這個小曲面塊的面積),過dS上任一點M作法線n= {A,B,C},當dS很小時，可以認為它是一塊以n為法線的平面(即S在點M處的切平面上的一塊)。設n與k(z軸上的單位矢量)不垂直(故cos<n,k>≠0)，則dS在xy平面上的投影為一面積元素
,依投影定理,有
1.設S:z= z(x,y)∈C1(Dxy)，
則S光滑且可取
,從而
2.設S由參數方程
不全為零,這時S光滑(所說的光滑曲面,均指這樣的曲面)，且可取n={A,B,C},又由二重積分的變數代換公式可知
把整個曲面表示為許多這樣的小曲面塊之並,每個小曲面塊的面積均用相應切平面塊的面積代替,並把整塊曲面的面積S認做這些小曲面塊面積之和當各個小曲面塊直徑的最大值趨於零時的極限,利用微元素法的思想可得曲面面積計算法,即分別把(5)~(8)式代人公式
