基本介紹
- 中文名:莫比烏斯帶
- 外文名:Möbius strip/Mobius Band
- 發現人:莫比烏斯和約翰·李斯丁
- 相似物:克萊因瓶
- 別名:莫比烏斯環
製作方法
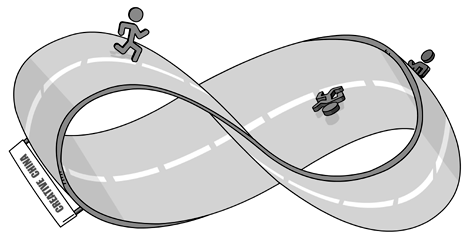 莫比烏斯圈
莫比烏斯圈和幾何學關係
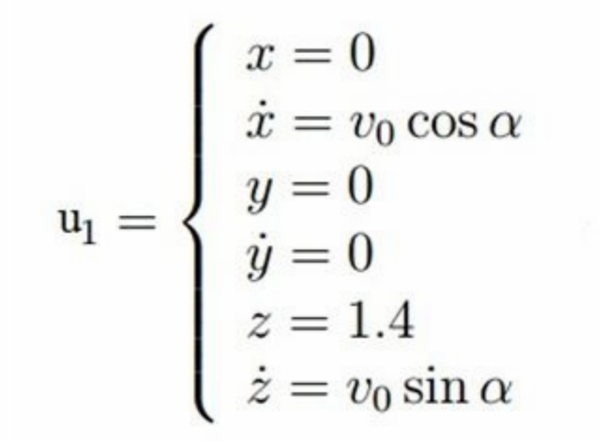 莫比烏斯帶的參數方程
莫比烏斯帶的參數方程拓撲變換
旋轉緯度的分析
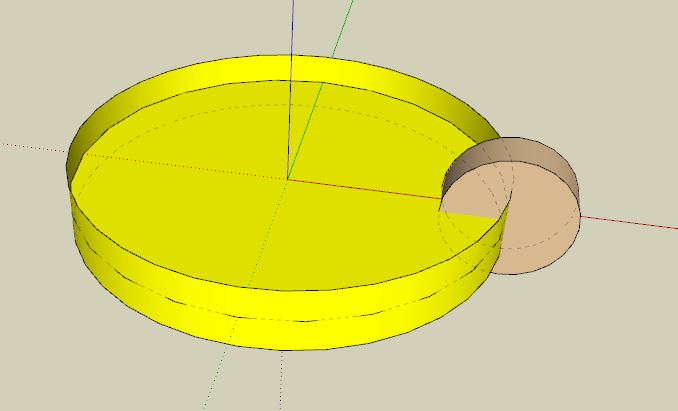 兩個旋轉緯度的關係
兩個旋轉緯度的關係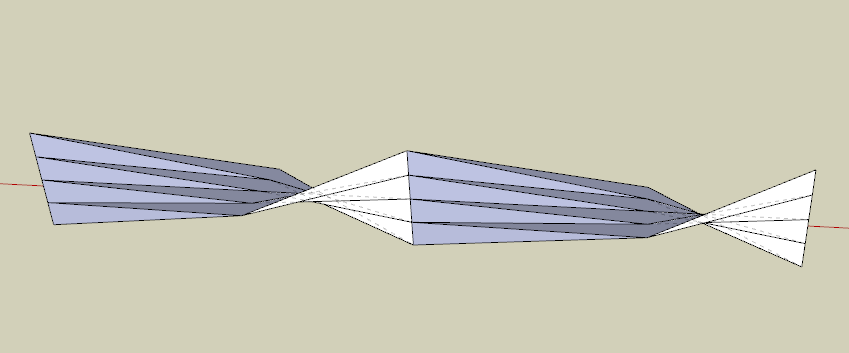 垂直方向上增加維度的示意
垂直方向上增加維度的示意
 莫比烏斯圈
莫比烏斯圈 莫比烏斯帶的參數方程
莫比烏斯帶的參數方程 兩個旋轉緯度的關係
兩個旋轉緯度的關係 垂直方向上增加維度的示意
垂直方向上增加維度的示意公元1858年,德國數學家莫比烏斯(Mobius,1790~1868)和約翰·李斯丁發現:把一根紙條扭轉180°後,兩頭再粘接起來做成的紙帶圈,具有魔術般的性質。普通紙帶具有兩個面...
莫比烏斯帶(德語:Möbiusband),又譯梅比斯環或麥比烏斯帶,是一種拓撲學結構,它只有一個面(表面),和一個邊界。它是由德國數學家、天文學家莫比烏斯(August ...
莫比烏斯指環是一種拓撲學結構,它只有一個面(表面),和一個邊界。它是由德國數學家、天文學家莫比烏斯(August Ferdinand Möbius)和約翰·李斯丁(Johhan Benedict ...
莫比烏斯最著名的成就是發現了三維歐幾里德空間中的一種奇特的二維單面環狀結構——後人稱為莫比烏斯帶。其他重要的成就包括在射影幾何中引進齊次坐標系、莫比烏斯變換...
《人和物理莫比烏斯帶上的世界》是2016年冶金工業出版社出版的圖書,作者是蔣志。...... 《人和物理莫比烏斯帶上的世界》是2016年冶金工業出版社出版的圖書,作者是蔣...
《莫比烏斯》由埃里克·羅查特執導,讓·杜雅爾丹、西西·迪·法蘭絲、蒂姆·羅斯等領銜主演。影片講述了聯邦安全局長官調查俄羅寡頭政治者洗錢黑幕的故事。...
默比烏斯變換(Mobius transformation),也稱莫比烏斯變換,是數論中的一種重要變換。默比烏斯變換是以數學家奧古斯特·費迪南德·莫比烏斯命名的, 它也被叫做homographic ...
但是這是一個不真實的傳聞,因為“∞”的發明比莫比烏斯帶還要早。∞無限符號的等式 在數學中,有兩個偶爾會用到的無限符號的等式,即:∞=∞+1,∞=∞×1。...
如果莫比烏斯帶能夠完美的展現一個“二維空間中一維可無限擴展之空間模型”的話,克萊因瓶只能作為展現一個“三維空間中二維可無限擴展之空間模型”的參考。因為在製作...
公元1858年,德國數學家莫比烏斯(Mobius,1790~1868)發現:把一個扭轉180°後再兩頭粘接起來的紙條,具有魔術般的性質。...
莫比烏斯帶是一種拓撲圖形,什麼是拓撲呢?拓撲所研究的是幾何圖形的一些性質,它們在圖形被彎曲、拉大、縮小或任意的變形下保持不變,只要在變形過程中不使原來不同...
不過這說法難以立足,因為無限大的符號“∞”比莫比烏斯帶出現得較早。與上述的例子相比,銜尾蛇的圖案在歷史上出現得更為之早,因此衍生出銜尾蛇與無限大符號之間...
只有一個側面的曲面(通常的曲面都有兩個側面),即不可定向的曲面,稱之為單側曲面(one-sided)。單側曲面並不多,一個著名的單側曲面是:莫比烏斯帶(Mobius Strip...
克萊茵曲面是由德國數學家克萊茵首先研究的,又稱克萊茵壺或克萊茵瓶,是一種單側曲面,克萊茵曲面亦是拓撲學的基本圖形之一。把兩個莫比烏斯帶沿著邊界黏合起來便...
克萊因瓶和莫比烏斯帶非常相像。 要想像克萊因瓶的結構,可先試想一個底部鏤空的紅酒瓶。現在延長其頸部,向外扭曲後伸進瓶子的內部,再與底部的洞相連線。 和我們...
不過這說法難以立足,因為無限大的符號“∞”比莫比烏斯帶出現得較早。與上述的例子相比,銜尾蛇的圖案在歷史上出現得更為之早,因此衍生出銜尾蛇與無限大符號之間...
三葉扭結是由莫比烏斯帶演變而成的。是由一條三稜柱帶經過三次盤繞,將其中的一端旋轉120゜後首尾相接,構成三面連通的單側單邊的三葉扭結造型。...
埃舍爾對拓撲學上有名的莫比烏斯帶很感興趣,以它創作了許多作品。我們知道,莫比烏斯帶有兩個重要的拓撲學 莫比烏斯帶Ⅰ 特性,一是沿其中線剪開,它不會分成兩個...
