假定一個法向量在某個空間中的光滑曲面上的一條閉曲線移動,並保持它是曲面的法向量,如果不管如何選擇閉曲線,當回到出發點時法向量的指向與它原來的指向總是一致的,則稱該曲面是雙側的。
基本介紹
- 中文名:雙側曲面
- 外文名:bilateral surface
- 套用學科:數學術語
- 範疇:數理科學
- 同類:單側曲面
- 涉及:曲面積分
概念





基本原理
性質
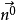


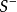
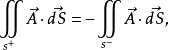
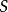
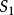

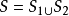



計算法

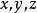


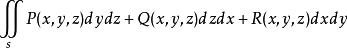
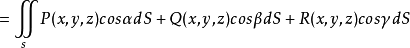
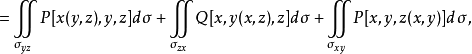
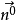
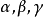


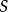


假定一個法向量在某個空間中的光滑曲面上的一條閉曲線移動,並保持它是曲面的法向量,如果不管如何選擇閉曲線,當回到出發點時法向量的指向與它原來的指向總是一致的,則稱該曲面是雙側的。





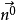


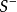
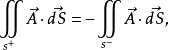
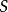
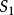

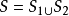






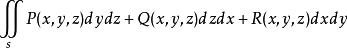
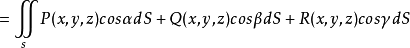
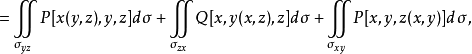
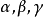


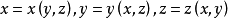

假定一個法向量在某個空間中的光滑曲面上的一條閉曲線移動,並保持它是曲面的法向量,如果不管如何選擇閉曲線,當回到出發點時法向量的指向與它原來的指向總是一致...
只有一個側面的曲面(通常的曲面都有兩個側面),即不可定向的曲面,稱之為單側曲面(one-sided)。單側曲面並不多,一個著名的單側曲面是:莫比烏斯帶(Mobius Strip...
克萊茵曲面是由德國數學家克萊茵首先研究的,又稱克萊茵壺或克萊茵瓶,是一種單側曲面,克萊茵曲面亦是拓撲學的基本圖形之一。把兩個莫比烏斯帶沿著邊界黏合起來便...
第二型曲面積分是關於在坐標面投影的曲面積分,其物理背景是流量的計算問題。第二型曲線積分與積分路徑有關,第二型曲面積分同樣依賴於曲面的取向,第二型曲面積分與...
曲面體層攝影是套用於口腔檢查的一種X線攝片技術,可檢查上頜、下頜、全口牙位三種位置。...
雙側牽張成骨下頜骨前徙術用於顱頜面骨牽引延長。 下頜牙根與下頜管的關係。...全口曲面斷層片,頦頂位片,必要時加照設計截骨線區的牙片,以取得精確的牽引器...
雙側牽張成骨下頜骨前移術用於顱頜面骨牽引延長。...... 雙側牽張成骨下頜骨前移術用於顱頜面骨牽引延長。...全口曲面斷層片,頦頂位片,必要時加照設計截骨線...
普通紙帶具有兩個面(即雙側曲面),一個正面,一個反面,兩個面可以塗成不同的顏色;而這樣的紙帶只有一個面(即單側曲面),一隻小蟲可以爬遍整個曲面而不必跨過它...
普通紙帶具有兩個面(即雙側曲面),一個正面,一個反面,兩個面可以塗成不同的顏色;而這樣的紙帶只有一個面(即單側曲面),一隻小蟲可以爬遍整個曲面而不必跨過它...
定理3 設空間區域V由分片光滑的雙側封閉曲面圍成。若函式SP,Q,R在V上連續,且有一階連續偏導數,則: ∫∫∫++=∂∂+∂∂+∂∂SVRdxdyQdzdxPdydzd...
