基本介紹
- 中文名:複流形
- 外文名:complex manifold
- 適用範圍:數理科學
定義






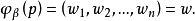





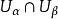

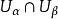
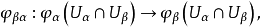









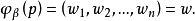





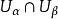

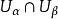
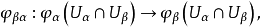


在數學中,特別是在微分幾何和代數幾何中,複流形是具有復結構的微分流形,即它能被一族坐標鄰域所覆蓋,其中每個坐標鄰域能與n維複線性空間中的一個開集同胚,從而...
殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有這種復結構是一個流形是殆複流形的必要不充分條件。每一個複流形都是一個...
《複流形和復結構的形變》是2008年3月1日世界圖書出版公司出版的圖書。本書是一部介紹複流形及其形變的經典入門書籍,不僅詳細講述了複流形上的形變理論,也...
在數學中,黎曼曲面是德國數學家黎曼為了給多值解析函式構想一個單值的定義域而提出的一種曲面。用現代的語言說,黎曼曲面就是連通的一維複流形。黎曼曲面的研究...
齊性複流形(homogeneous complex manifold)復的齊性流形.以H(M)表示複流形M的全純變換群.若有實李群G}H(M)可遞地作用於M上,則稱M為齊性複流形,並稱M...
鐸爾博爾復形(Dolbeault complexes)是由複流形的C模序列與運算元構成的復形。...... 鐸爾博爾復形(Dolbeault complexes)是由複流形的C模序列與運算元構成的復形。...
《複流形上的微分分析》是2004年世界圖書出版公司出版的圖書,作者是R.O.WELLS.Jr。...... 《複流形上的微分分析》是2004年世界圖書出版公司出版的圖書,作者是R...
所謂霍普夫流形(Hppf manifold),是指與S2n+1×S1同胚的複流形。...... 霍普夫流形是特殊的複流形。所謂霍普夫流形,是指與S2n+1×S1同胚的複流形。若n=1,...
《多複分析與複流形引論》是2010年北京大學出版社出版的圖書,作者是譚小江。該書主要內容是高數裡面的多複分析與複流形引論 ,是為大學基礎數學專業高年級本科生和...
克勒流形是一類重要的複流形,具有克勒度量的複流形稱為克勒流形。例如,Cn中有界域關於伯格曼度量為克勒流形。...
施坦流形是從多複變函數論角度研究最多的複流形,它是全純凸域在複流形上的推廣。...... 施坦流形是從多複變函數論角度研究最多的複流形,它是全純凸域在...
埃爾米特流形是一類重要的複流形,具有埃爾米特度量的複流形稱為埃爾米特流形。...... 埃爾米特流形是一類重要的複流形,具有埃爾米特度量的複流形稱為埃爾米特流...
在數學中,一個凱勒流形(Kähler manifold)是具有滿足一個可積性條件的酉結構(一個U(n)-結構)的流形。特別地,它是一個黎曼流形 、複流形以及辛流形,這三...
對稱埃爾米特流形是一類重要的複流形。多複變函數論中第一個系統的分類工作是嘉當(Cartan,E)給出的,他給出了對稱埃爾米特空間在全純等價下的分類。...
本書作者以微分流形為中心寫了這本書,涉及拓撲學的廣泛的領域並在分析數學、幾何學乃至理論物理學中均可得到重要的套用。本書的主要內容是:微分流形、示性類...
代數流形(algebraic manifold)是復射影空間中的代數子集。若P(C)的一個子流形是P(C)的一個代數子集,則稱這個復子流形為代數子流形。若一個複流形是雙全...
微分流形(differentiable manifold),也稱為光滑流形(smooth manifold),是拓撲學和幾何學中一類重要的空間,是帶有微分結構的拓撲流形。 微分流形是微分幾何與微分...
復n何(complex geometry)複流形上的幾何學.複流形是具有復結構的微分流形,即局部地它能與n維複數空間C"的一個開鄰域解析同胚.因此,一個n維複流形自然也是2n...
作為一維複流形,黎曼曲面可以由兩個圖卡描述,每個的定義域都是複數平面C.令ζ和ξ為C上的復坐標。將非零複數ζ和非零複數ξ用如下轉移映射等同起來:ζ = 1 ...
設M是一個複流形,X是M的真解析子集,若對於每個x∈X,存在U∈Ux和f∈A(U),使得x∩U=f-1(0),則稱x為M的解析超曲面。...
全純映射(holomorphic map)是複流形上的一種有解析性的映射。映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G的定義域D(G)為X...
復二次超曲面(complex quadric)是復射影空間中的特殊超曲面。復射影空間是實射影空間在復情形的推廣,是一種典型的複流形。特別地,當n=1時,P(C)是普通2維...
卡拉比猜想可以認為是單值化定理在高維不可思議的大膽推廣,竟然給出了高維複流形中難得一見的一般規律。特別的是它在復卡勒流形的第一陳類大於零、等於零和...
殆復結構,也稱近復結構,它是殆複流形上的一種特殊結構。殆複流形是一個在每一個點的切空間上有個光滑的線性的復結構的光滑流形。流形有殆復結構是一個流...
李群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。在數學中,李群(Lie group)是具有群結構的實流形或者複流形,並且群...
對於1維以上的復向量叢,陳類不是一個完全不變數。近複流形的陳類和配邊(cobordism)陳類的理論導致了近複流形的配邊不變數的研究。...
