鐸爾博爾復形

鐸爾博爾復形（Dolbeault complexes）是由複流形的C模序列與運算元構成的復形。

基本介紹

• 中文名：鐸爾博爾復形
• 外文名：Dolbeault complexes
• 適用範圍：數理科學

簡介

鐸爾博爾復形是由複流形的C模序列與運算元∂與構成的復形。

設X是n維複流形，對於p,q≥0，有下述鐸爾博爾復形

其中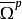表示反全純叢Λ^0,qX'的反全純截面的芽層。

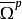
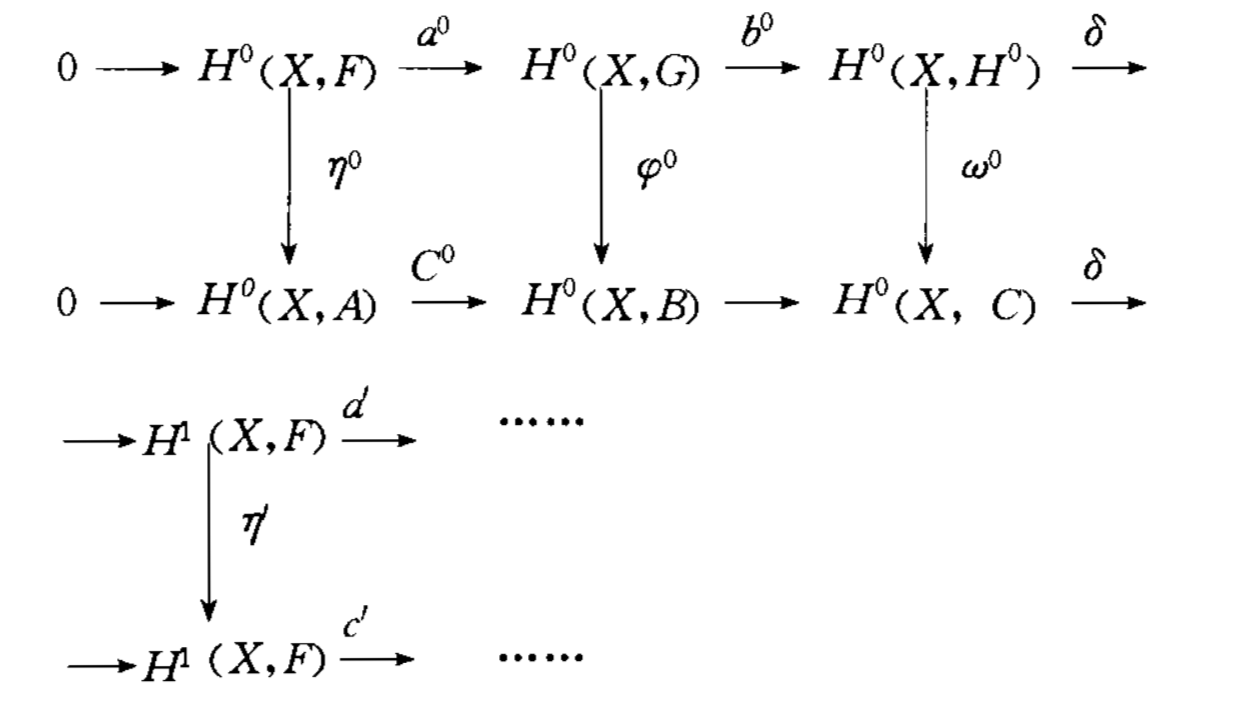圖1

複流形

在數學中，特別是在微分幾何和代數幾何中，複流形是具有復結構的微分流形，即它能被一族坐標鄰域所覆蓋，其中每個坐標鄰域能與n維複線性空間中的一個開集同胚，從而使坐標區域中的點具有復坐標 (z1,…,zn)，而對兩個坐標鄰域的重疊部分中的點，其對應的兩套復坐標之間的坐標變換是全純的。稱n為此複流形的復維數。

一個n維複流形也是2n維的（實）微分流形。

復形

復形是組合拓撲的基本概念之一，許多種拓撲空間的研究都可化歸為復形拓撲性質的研究，復形是不同維的正常分布的單純形之總和，即復形中任意兩個單純形，或不相交，或僅具有公共邊界等。

此外，復形中單純形所有邊界均屬於單純形，復形中單純形最高維數稱之為復形的維數。