基本介紹
- 中文名:復形
- 外文名:complex
- 別稱:單純復形,幾何單純復形等
- 所屬學科:數學
- 所屬問題:組合拓撲(單純同調論)
基本介紹



單純復形的連通性



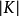
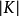

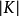



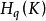



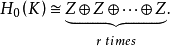
相關定義與定理
單純形
單純形




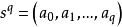
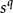



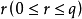

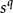
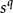








 圖1 3維單形(四面體)
圖1 3維單形(四面體)有向單形與無向單形

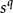

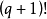
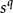
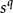

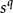





單純複合形(復形)



 圖2 規則相處
圖2 規則相處 圖3 不規則相處
圖3 不規則相處



 圖4 復形
圖4 復形 圖5 非復形
圖5 非復形有向單形的基本組



鏈

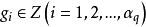
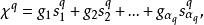

鏈邊界






















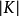

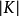



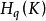



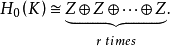




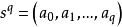
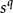



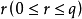

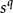
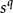








 圖1 3維單形(四面體)
圖1 3維單形(四面體)
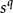

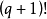
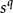
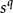

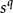








 圖2 規則相處
圖2 規則相處 圖3 不規則相處
圖3 不規則相處



 圖4 復形
圖4 復形 圖5 非復形
圖5 非復形



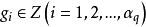
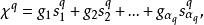





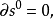











復形是組合拓撲的基本概念之一,許多種拓撲空間的研究都可化歸為復形拓撲性質的研究,復形是不同維的正常分布的單純形之總和,即復形中任意兩個單純形,或不相交,...
抽象復形是幾何復形的一種抽象。將幾何單純復形的一些良好性質,利用同構復形的思想,加以抽象化就得到抽象復形的概念,同構的復形對應同一個抽象復形。...
單純復形(Simplicial Complex)是拓撲學中的概念,指由點、線段、三角形等單純形“粘合”而得的拓撲對象。單純復形不應當與範疇同倫論中的單純集合混淆。單純復形...
上復形亦稱上鏈一種特殊的模同態序列.設有A一同態序列...... 上復形亦稱上鏈一種特殊的模同態序列.設有A一同態序列 上復形(cocomplex)亦稱上鏈一種特殊的模...
CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的空間。...... CW復形是由一些(有限多個或無窮多個)胞腔從低維到高維逐層堆積而成的...
鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈...
列維形式(Levi form)是復形的(1,1)微分形式。復形是組合拓撲的基本概念之一。...... 列維形式(Levi form)是復形的(1,1)微分形式。復形是組合拓撲的基本概念...
上同調運算(cohomology operations)作用在上同調群上的一種自然變換,它是代數拓撲學中的一個重要工具。在同調論中,上同調是對一個在上鏈復形(co-chain)上定義一...
對於一個以 A 為頂點集的抽象復形 𝓚,復形 𝓚 中的元素稱為復形 𝓚 的抽象單形。...
}取遍單純復形K的所有單形,且每個單形取好了定向(0維單形不取定向),αi為整數(即線性組合中的每一項是K中的一個n維定向單形,且附一個整係數)。兩個n維...
懷特海定理(Whitehead theorem)同倫論中一條重要的定理.懷特海定理斷言:若X,Y都是CW復形,則連續映射.f : X->Y是同倫等價若且唯若它是弱同倫等價.該定理...
跰趾,又稱“復甲”、“跰甲”,在醫學上稱作瓣狀甲(petaloidtoenails,PTN)或小腳趾復形,是指小腳趾甲分瓣而非完整一塊。實際上瓣狀甲是一個常染色體顯性性狀,不...
第1、2兩章是關於單純同調論的基本內容,主要介紹復形、單純映射和單純同調群等理論,它們將為第6章奇異同調論的學習,作適當“熱身”,並為學習第3章曲面的拓撲...
稱為一個復形,若 ,這一復形記作 叫作n循環, 叫作n邊緣。由復形的定義條件 , 叫作第n個同調模。如果對任意整數n, ,換言之, ,則稱 是一個正合列。...
→ Em→0 其中的每個箭頭都是微分運算元,其符號構成一個正合復形。當這個復形只有有兩項非零時,前述條件等價於其間的運算元是橢圓的,因此橢圓運算元是橢圓復形的...
