鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。
類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些對象有許多共同特徵。
基本介紹
- 中文名:鏈復形
- 外文名:chain complex
- 領域:數學
- 性質:抽象的復形
- 實質:特殊的模同態序列
- 群:鏈群
概念
上復形
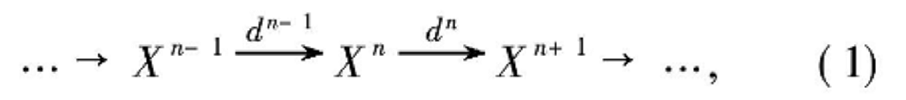

同態

鏈群



鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。
類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些對象有許多共同特徵。
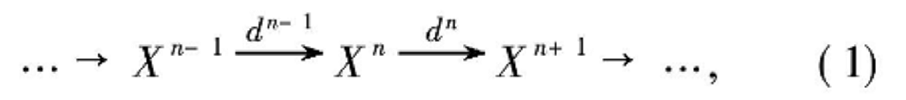





鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈...
德拉姆復形(de Rham complex)是一種與微分形式相關的鏈復形,亦稱為德拉姆鏈復形。...... 德拉姆復形(de Rham complex)是一種與微分形式相關的鏈復形,亦稱為...
1. 有序鏈復形與H4(AP)P≥5Adams譜序列中的乘積 .國家圖書館.2014-06-29[引用日期2014-06-29] 詞條標籤: 文化 V百科往期回顧 詞條統計 瀏覽次數:次 編...
上同調運算(cohomology operations)作用在上同調群上的一種自然變換,它是代數拓撲學中的一個重要工具。在同調論中,上同調是對一個在上鏈復形(co-chain)上定義一...
對上鏈復形的上同調亦同,此時連線同態的方向是 。這類序列稱作長正合序列,它是同調代數最重要的技術之一。在代數拓撲中,長正合序列與相對同調群和Mayer-...
同調泛係數定理(the universal coefficientstheorem for homology)闡明一般係數群的同調群與整係數同調群之間關係的定理.若c一}CP,tJP)是鏈復形,G是任意交換群,則...
都是同構。上鏈復形間的態射 被稱為擬同構,如果它所誘導的所有上同調群間的同態 都是同構。擬同構給出導出範疇中的同構。 [1] 擬...
奇異上同調(singular cohomology)一種上同調群.設(X,A)是空間偶,G是任意交換群.記C(X,A)表示(X,A)的奇異鏈復形.定義(X,A)的係數在G中的q維奇異上鏈...
標準單形是一類特殊的單形,它在研究復形性質及奇異同調理論時都要用到。...... 到X連續映射稱為X的q維奇異單形(singular simplex)。拓撲空間X的奇異鏈復形(si...
2胞腔鏈復形與胞腔鏈映射 3胞腔同調定理 3.1胞腔同調定理 3.2胞腔同調定理的推論 3.3帶係數的胞腔同調與胞腔上同調 3.4單純復形與單純映射 3.5單純鏈復...
上積是定義在拓撲空間奇異上鏈復形及奇異上同調群中的一種乘法。上積上同調群的上積 編輯 設X 是一個拓撲空間,奇異上鏈復形的上積...
39 伽復形的同調40 套用:射影空間和誘鏡空間第五章 上同調41 Hom函子42 單純上同調群43 相對上同調44 上同調論45 自由鏈復形的上同調...
6.1 鏈復形·鏈映射·鏈同倫習題6.2 奇異同調群習題6.3 奇異同調群的同倫不變性習題6.4 Mayer-Vietoris序列習題6.5 同調論的一些套用...
格爾斯滕哈伯代數是Gerstenhaber在研究結合代數的形變時發現的。一個結合代數的形變跟它的Hochschild上復形有密切的關係,Gerstenhaber證明,Hochschild上復形實際上形成...
數學裡,單純集合(simplical set)是範疇同倫論中一個構造,這是“良態”拓撲空間的一個純代數模型。歷史上,這個模型源自組合拓撲學特別是單純復形。...
